
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2) Ta có: \(\left|4-3x\right|=\left|x+\dfrac{1}{3}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4-3x=x+\dfrac{1}{3}\\3x-4=x+\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-4x=-\dfrac{11}{3}\\2x=\dfrac{13}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{12}\\x=\dfrac{13}{6}\end{matrix}\right.\)
3: Ta có: \(\left|5x-2\right|-\left|3x+\dfrac{1}{2}\right|=0\)
\(\Leftrightarrow\left|5x-2\right|=\left|3x+\dfrac{1}{2}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-2=3x+\dfrac{1}{2}\\5x-2=-3x-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{5}{2}\\8x=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{3}{16}\end{matrix}\right.\)
4: Ta có: \(\left|2x-1\right|=x+\dfrac{4}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+\dfrac{4}{3}\left(x\ge\dfrac{1}{2}\right)\\1-2x=x+\dfrac{4}{3}\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=\dfrac{4}{3}+1\\-2x-x=\dfrac{4}{3}-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\-3x=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{1}{9}\end{matrix}\right.\)

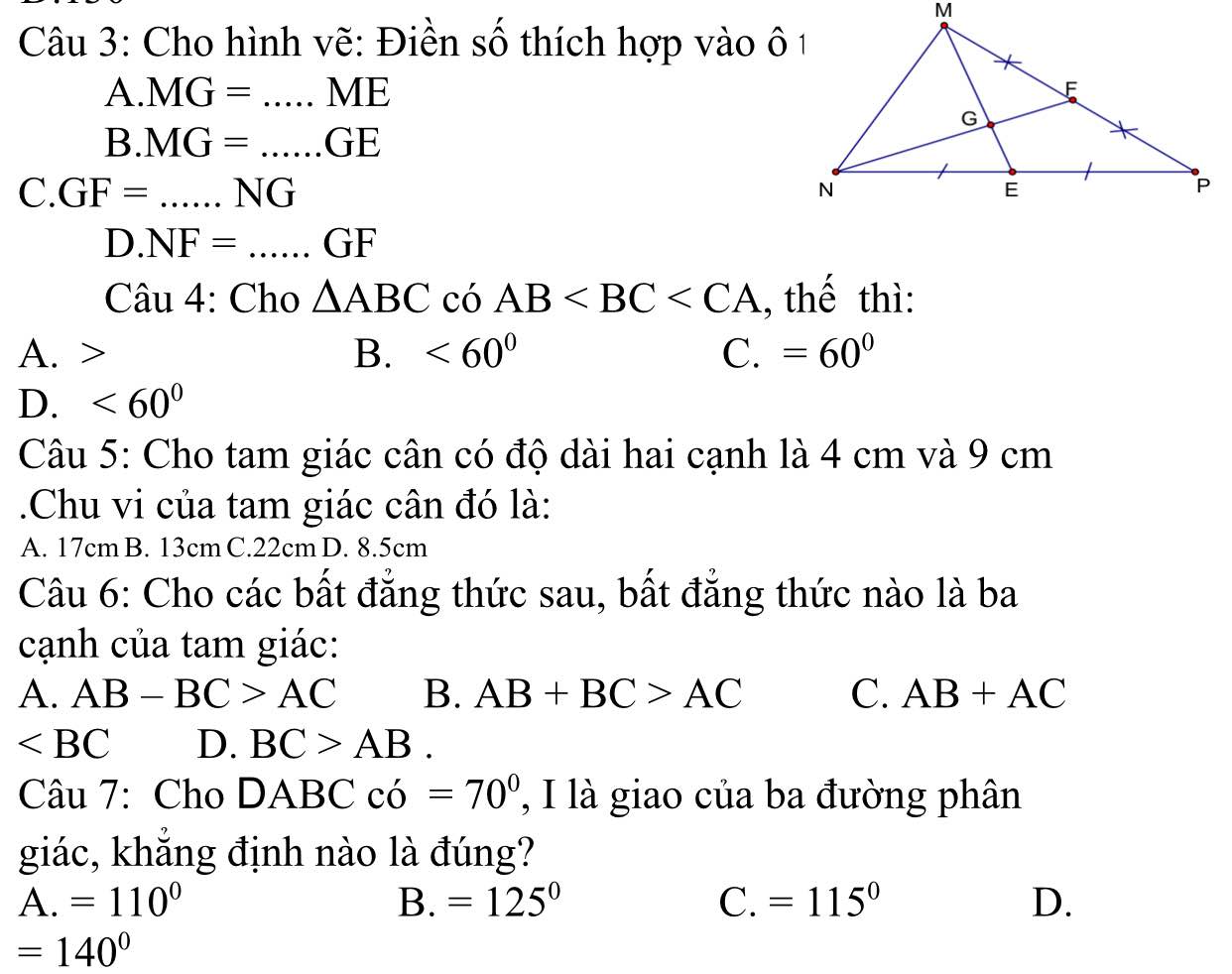
Câu 3:
a) \(MG=\dfrac{2}{3}ME\)
b) MG=2GE
Câu 5: C
Câu 6: B

a, Xét tam giác ABM và tam giác CDM có: góc AMB= góc CMD( đối đỉnh)
AM=CM(gt)
BM=DM(gt)
suy ra tam giác ABM= tam giác CDM(c.g.c)

\(x+\dfrac{3}{5}=\left(-\dfrac{2}{5}\right)^2\\ x+\dfrac{3}{5}=\dfrac{4}{25}\\ x=\dfrac{4}{25}-\dfrac{3}{5}\\ x=\dfrac{4}{25}-\dfrac{15}{25}\\ x=-\dfrac{11}{25}\)
__
\(\left|x+\dfrac{3}{4}\right|-\dfrac{5}{6}=0\\ \left|x+\dfrac{3}{4}\right|=0+\dfrac{5}{6}\\ \left|x+\dfrac{3}{4}\right|=\dfrac{5}{6}\\ \left|x+\dfrac{3}{4}\right|=\pm\dfrac{5}{6}\\ \left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{5}{6}\\x+\dfrac{3}{4}=-\dfrac{5}{6}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{5}{6}-\dfrac{3}{4}\\x=-\dfrac{5}{6}-\dfrac{3}{4}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{20}{24}-\dfrac{18}{24}\\x=-\dfrac{20}{24}-\dfrac{18}{24}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{2}{24}\\x=-\dfrac{38}{24}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{1}{12}\\x=-\dfrac{19}{12}\end{matrix}\right.\)
__
\(\left(x+\dfrac{3}{7}\right)^2=\dfrac{25}{49}\\ \left(x+\dfrac{3}{7}\right)^2=\left(\pm\dfrac{5}{7}\right)^2\\ \left[{}\begin{matrix}x+\dfrac{3}{7}=\dfrac{5}{7}\\x+\dfrac{3}{7}=-\dfrac{5}{7}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{5}{7}-\dfrac{3}{7}\\x=-\dfrac{5}{7}-\dfrac{3}{7}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{2}{7}\\x=-\dfrac{8}{7}\end{matrix}\right.\)
Câu 2:
a: x=4/25-3/5=4/25-15/25=-11/25
b: =>|x+3/4|=5/6
=>x+3/4=5/6 hoặc x+3/4=-5/6
=>x=5/6-3/4=10/12-9/12=1/12 hoặc x=-10/12-9/12=-19/12
c: =>x+3/7=5/7 hoặc x+3/7=-5/7
=>x=-8/7 hoặc x=2/7

a) \(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{310}{10}=31\)
a=62
b =93
c =155
b) 2x = 3y =>\(\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{310}{5}=62\)
x =3.62 =186
y =2 . 62 =124


d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC

`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }x+y=50\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/3 = (x+y)/(2 + 3) = 50/5 = 10`
`=> x/2 = y/3 = 10`
`=> x = 10*2 = 20; y = 3*10 = 30`
Vậy, `x = 20; y = 30`
`b)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }5x+4y=110\)
Ta có:
`x/2 = y/3` `=> (5x)/10 = (4y)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(5x)/10 = (4y)/12 = (5x+4y)/(10 + 12) = 110/22 = 5`
`=> x/2 = y/3 = 5`
`=> x = 2*5 = 10; y = 3*5 = 15`
Vậy, `x = 10; y = 15`
`c)`
\(5x=11y\text{ và }2x+3y=37\)
Ta có:
`5x = 11y -> x/11 = y/5 -> (2x)/22 = (3y)/15`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(2x)/22 = (3y)/15 = (2x+3y)/(22+15) = 37/37 = 1`
`=> x/11 = y/5 = 1`
`=> x = 11; y = 5`
Vậy, `x = 11; y = 5`
`d)`
\(\dfrac{x}{2}=\dfrac{y}{1}\text{và }x+y-63=0\)
Ta có: `x + y - 63 = 0 -> x + y = 63`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/1 = (x+y)/(2+1) = 63/3 = 21`
`=> x/2 = y/1 = 21`
`=> x = 21*2 =42; y = 21`
Vậy, `x = 42; y = 21.`
`2,`
`a)`
\(\dfrac{a}{14}=\dfrac{b}{2}=\dfrac{c}{4}\text{ và }a+b+c=5\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`a/14 = b/2 = c/4 = (a+b+c)/(14+2+4)=5/20=1/4=0,25`
`=> a/14 = b/2 = c/4 = 0,25`
`=> a = 14*0,25 = 3,5` `; b = 2*0,25 = 0,5;` `c = 4*0,25 = 1`
Vậy, `a = 3,5`; `b = 0,5`; `c = 1`
`b)`
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\text{ và }7a+3b-5c=7\)
Ta có:
`a/3 = b/5 = c/8 => (7a)/21 = (3b)/15 = (5c)/40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(7a)/21 = (3b)/15 = (5c)/40 = (7a + 3b - 5c)/(21 + 15 - 40)=7/-4 = -1,75`
`=> a/3 = b/5 = c/8 = -1,75`
`=> a = 3*(-1,75) = -5,25`
`b = 5*(-1,75) = -8,75`
`c = 8*(-1,75) = -14`
Vậy, `a = -5,25; b = -8,75`; `c = -14`
`c)`
\(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\text{và }3a+b-2c=14\)
Ta có:
`a/3 = b/8 = c/5 -> (3a)/9 = b/8 = (2c)/10`
Câu này bạn làm tương tự nha
`d)`
\(\dfrac{a}{3}=\dfrac{b}{2};\dfrac{b}{7}=\dfrac{c}{5}\text{ và }3a+5c-7b=30\)
Ta có:
`a/3 = b/2 -> a/21 = b/14`/
`b/7 = c/5 -> b/14 = c/10`
`=> a/21 = b/14 = c/10`
`=> (3a)/63 = (7b)/98 = (5c)/50`
Câu này bạn cũng làm tương tự.
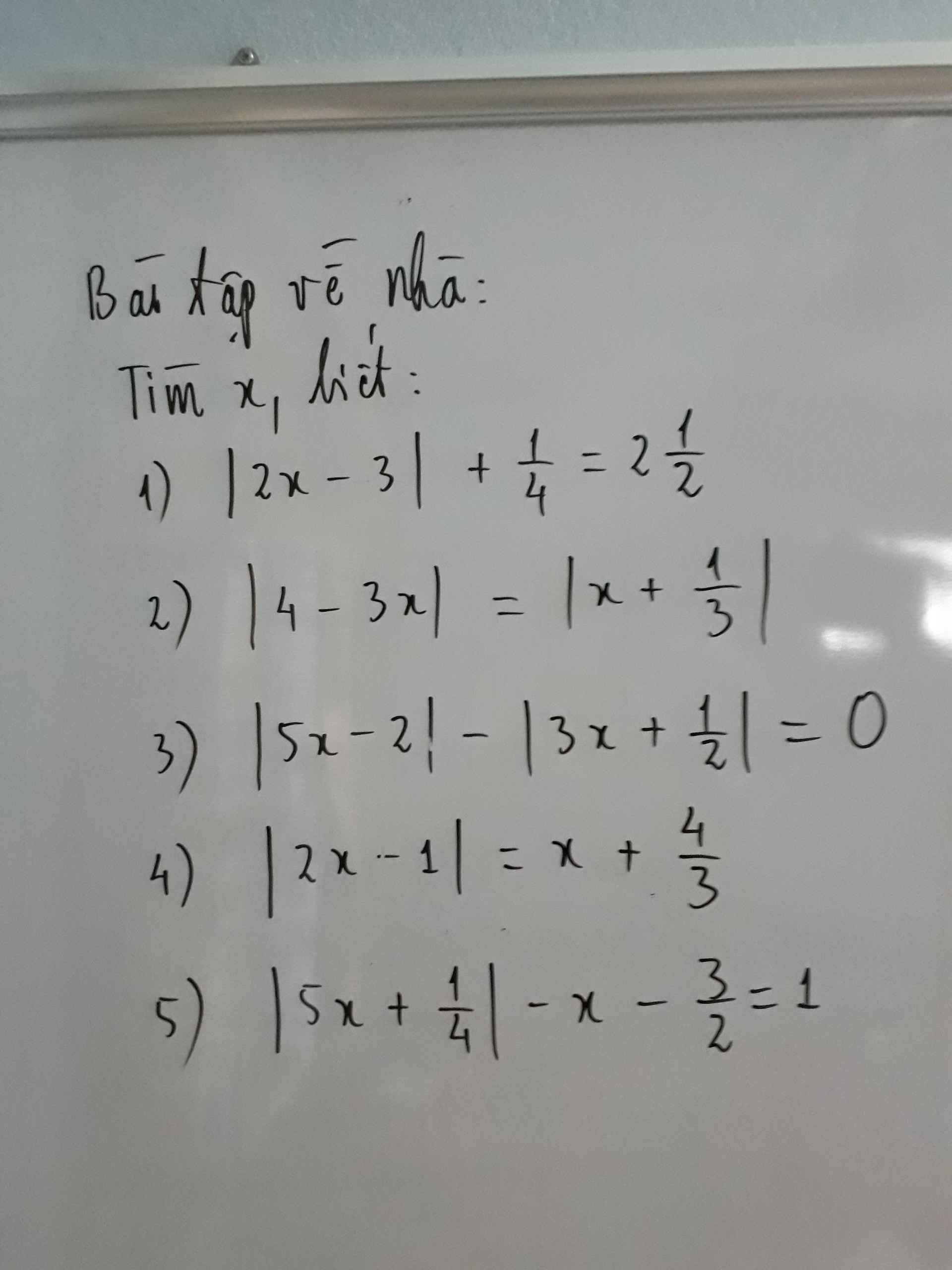

 mn giúp mình câu c và d thôi ạ
mn giúp mình câu c và d thôi ạ
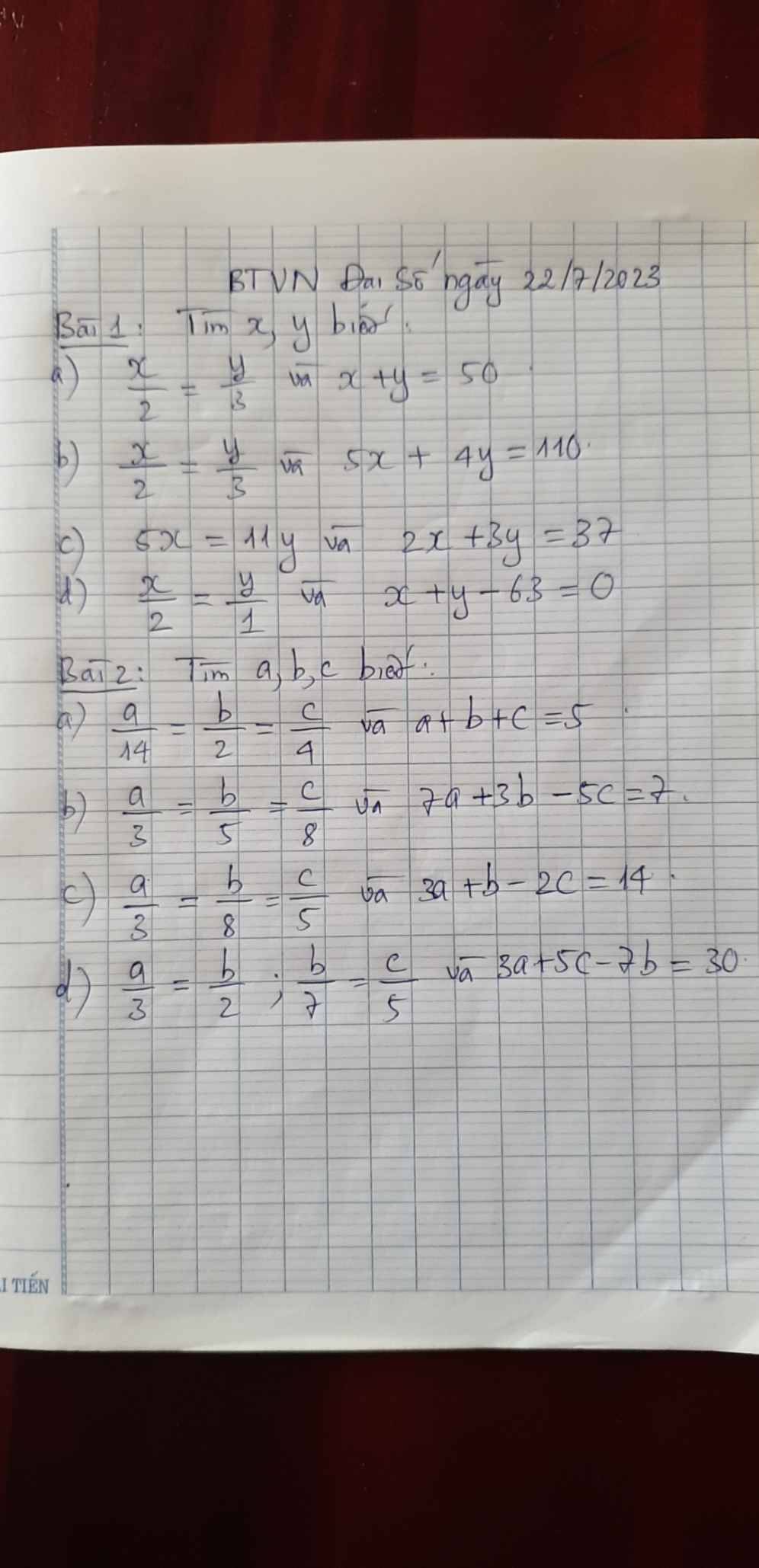
lỗi r, cập nhập lại ik bạn
lx