
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta thấy các PS đều có dạng: \(\dfrac{1}{1+\left(n+2\right)},\dfrac{2}{2+\left(n+2\right)},...,\dfrac{p-2}{p-2+\left(n+2\right)},\dfrac{p-1}{p-1+\left(n+2\right)}\)Tức là có dạng \(\dfrac{p}{p+\left(n+2\right)}\)
⇒ p và n+2 là nguyên tố cùng nhau
Thế thì p là số nguyên tố nào z


Đặt \(\dfrac{x}{4}=\dfrac{y}{7}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=7k\end{matrix}\right.\)
Ta có: xy=112
\(\Leftrightarrow28k^2=112\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=4\cdot2=8\\y=7k=7\cdot2=14\end{matrix}\right.\)
Trường hợp 2: x=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-8\\y=7k=-14\end{matrix}\right.\)

\(a.720:\left(x-17\right)=12\)
\(x-17=60\)
\(x=77\)
\(b.\left(x-28\right):12=8\)
\(x-28=96\)
\(x=124\)
\(c.26+8x=6x+46\)
\(8x-6x=46-26\)
\(2x=20\)
\(x=10\)
\(d.3600:\left[\left(5x+335\right):x\right]=50\)
\(\left(5x+335\right):x=72\)
\(5+335:x=72\)
\(335:x=67\)
\(x=5\)
a) \(720:\left(x-17\right)=12\)
\(\Rightarrow x-17=\dfrac{720}{12}\)
\(\Rightarrow x-17=60\)
\(\Rightarrow x=60+17\)
\(\Rightarrow x=77\)
b) \(\left(x+28\right):12=8\)
\(\Rightarrow x+28=12\cdot8\)
\(\Rightarrow x+28=96\)
\(\Rightarrow x=96-28\)
\(\Rightarrow x=68\)
c) \(26+8x=6x+46\)
\(\Rightarrow8x-6x=46-26\)
\(\Rightarrow2x=20\)
\(\Rightarrow x=\dfrac{20}{2}\)
\(\Rightarrow x=10\)
d) \(3600:\left[\left(5x+335\right):x\right]=50\)
\(\Rightarrow\left(5x+335\right):x=\dfrac{3600}{50}\)
\(\Rightarrow\left(5x+335\right):x=72\)
\(\Rightarrow5x+335=72\cdot x\)
\(\Rightarrow72x-5x=335\)
\(\Rightarrow67x=335\)
\(\Rightarrow x=\dfrac{335}{67}\)
\(\Rightarrow x=5\)

Ta có: \(14x=21y=16z\)=> \(\frac{x}{\frac{1}{14}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\) => \(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}=\frac{2x+y-z}{\frac{1}{7}+\frac{1}{21}-\frac{1}{16}}=\frac{2}{\frac{43}{336}}=\frac{672}{43}\)
=> \(\hept{\begin{cases}\frac{x}{\frac{1}{14}}=\frac{672}{43}\\\frac{y}{\frac{1}{21}}=\frac{672}{43}\\\frac{z}{\frac{1}{16}}=\frac{672}{43}\end{cases}}\) => \(\hept{\begin{cases}x=\frac{672}{43}.\frac{1}{14}=\frac{48}{43}\\y=\frac{672}{43}.\frac{1}{21}=\frac{32}{43}\\z=\frac{672}{43}.\frac{1}{16}=\frac{42}{43}\end{cases}}\)
Vậy ...
\(\Rightarrow\frac{x}{\frac{1}{14}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
\(\Rightarrow\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}\)
+ Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{\frac{1}{7}}=\frac{y}{\frac{1}{21}}=\frac{z}{\frac{1}{16}}=\frac{2x+y-z}{\frac{1}{7}+\frac{1}{21}-\frac{1}{16}}=\frac{2}{\frac{43}{336}}=\frac{672}{43}\)
Suy ra \(\frac{2x}{\frac{1}{7}}=\frac{672}{43}\Rightarrow x=\frac{48}{43}\)
\(\frac{y}{\frac{1}{21}}=\frac{672}{43}\Rightarrow y=\frac{32}{43}\)
\(\frac{z}{\frac{1}{16}}=\frac{672}{43}\Rightarrow z=\frac{42}{43}\)
Vậy \(x=\frac{48}{43};y=\frac{32}{43};z=\frac{42}{43}\)
Chúc bạn học tốt !!!

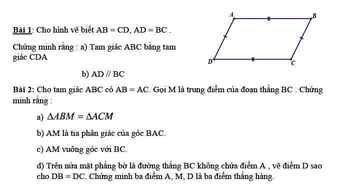
Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!

Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$
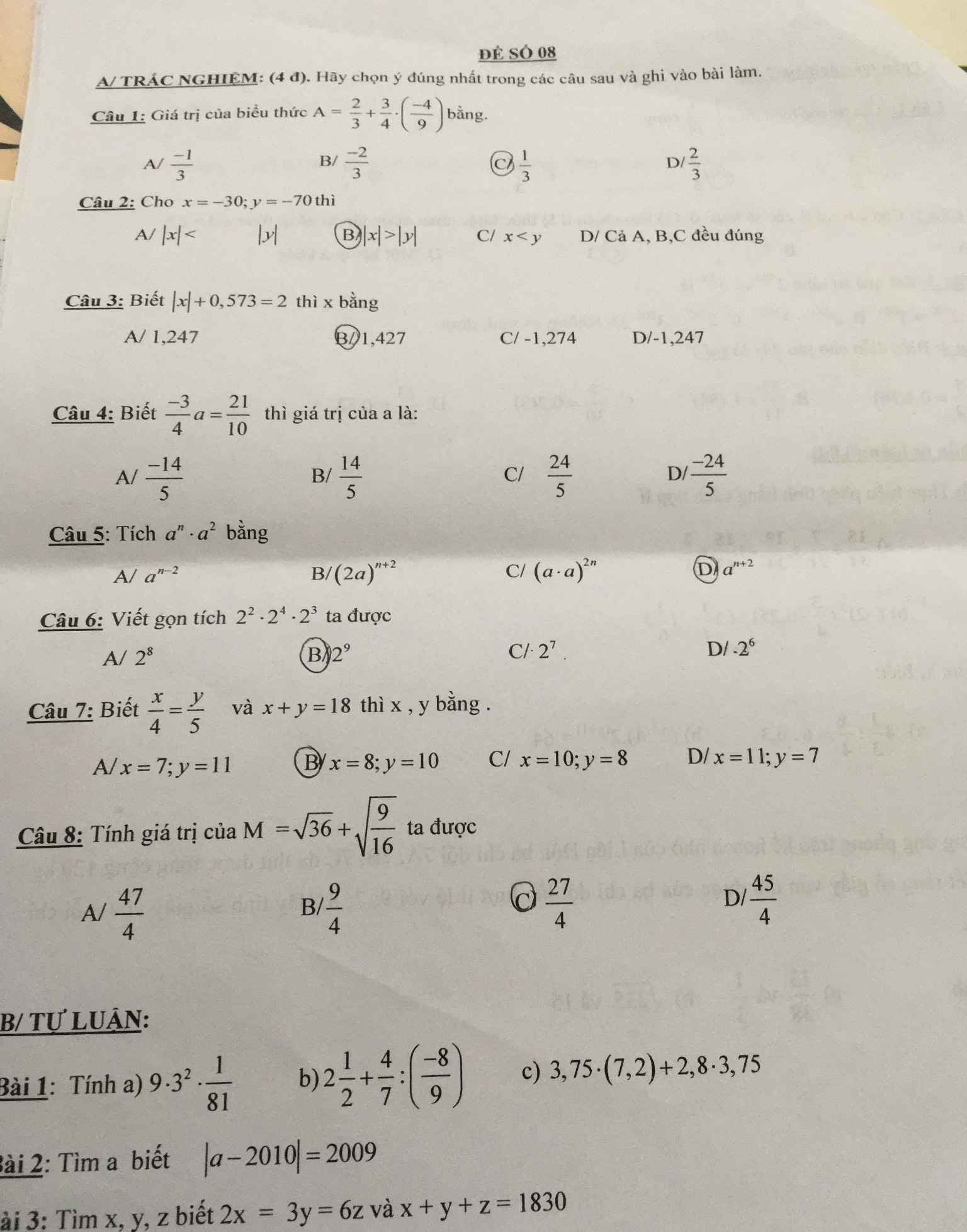


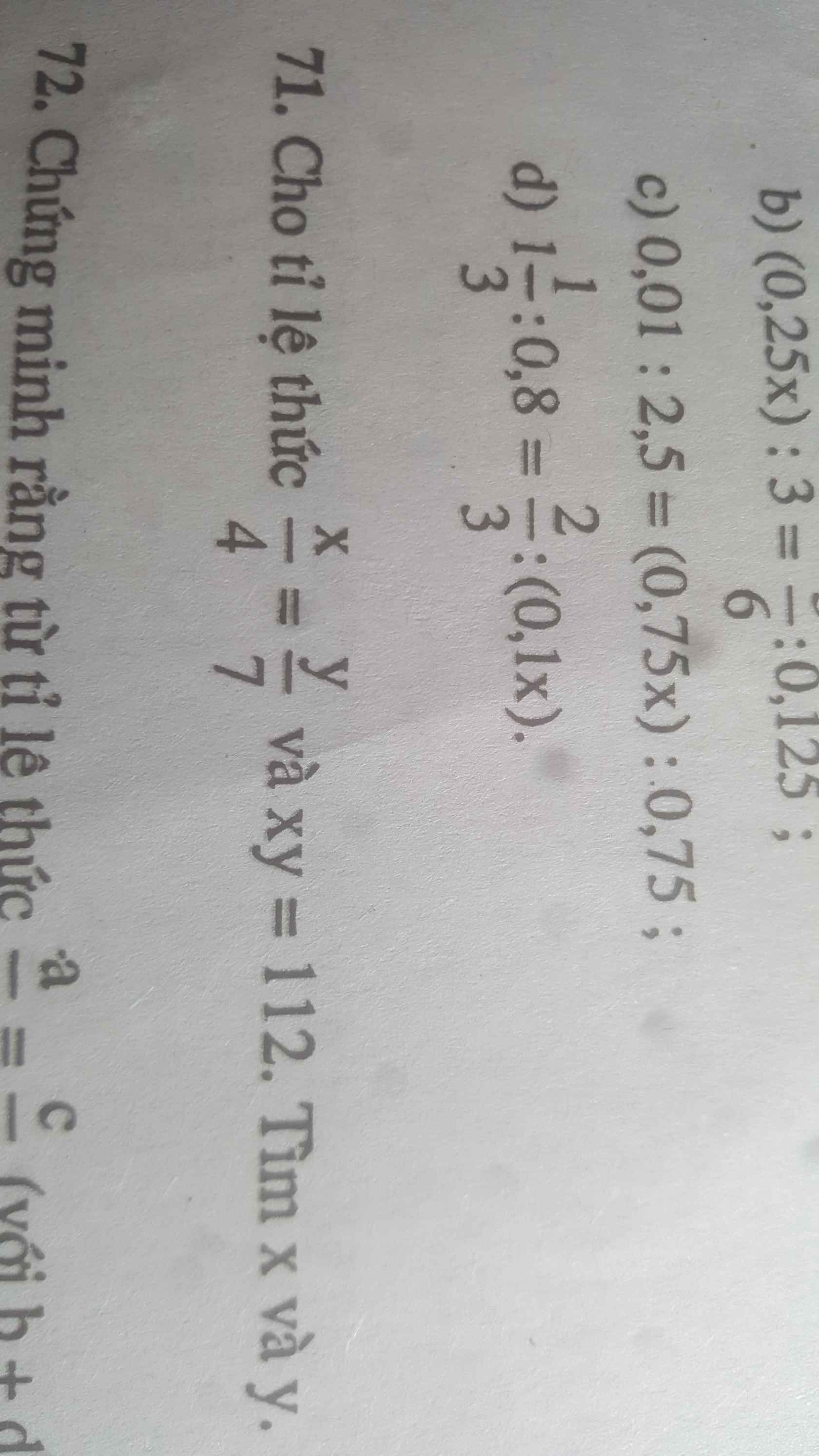



e cảm ơn ạ