
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
\(x^2+2x+m+1\le0\)
\(\Leftrightarrow m\le f\left(x\right)=-\left(x+1\right)^2\)
Yêu cầu bài toán thỏa mãn khi:
\(\Leftrightarrow m\le maxf\left(x\right)=max\left\{f\left(-1\right);f\left(3\right)\right\}=0\)
Vậy \(m\le0\)
3.
\(f\left(x\right)=x^2-2mx-3m\le0\)
Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta'\ge0\\f\left(-1\right)\le0\\f\left(3\right)\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+3m\ge0\\1-m\le0\\-9m-9\le0\end{matrix}\right.\Leftrightarrow m\ge1\)
Vậy \(m\ge1\)

Pt có 2 nghiệm khi: \(\left\{{}\begin{matrix}m\ne0\\\Delta'=9\left(m-1\right)^2-9m\left(m-3\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\m\ge-1\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{6\left(m-1\right)}{m}\\x_1x_2=\dfrac{9\left(m-3\right)}{m}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Rightarrow\dfrac{6\left(m-1\right)}{m}=\dfrac{9\left(m-3\right)}{m}\)
\(\Rightarrow6\left(m-1\right)=9\left(m-3\right)\)
\(\Rightarrow m=7\)
A đúng


Hàm xác định trên R khi và chỉ khi:
\(\left\{{}\begin{matrix}a=2>0\\\Delta'=m^2-2m\le0\end{matrix}\right.\)
\(\Leftrightarrow0\le m\le2\)
\(\Rightarrow m_{max}=2\) ; \(m_{min}=0\)


Bài 20
Hệ (1) ⇔ \(\left\{{}\begin{matrix}1< x< 4\\x\le m-1\end{matrix}\right.\)
Đặt hai tập hợp A = (1 ; 4) và B = (\(-\infty\); m - 1]
Nếu m - 1 ≤ 1 tức m ≤ 2 thì A \(\cap\) B = ∅, hệ vô nghiệm
Nếu 1 < m - 1 < 4 tức 2 < m < 5 thì
A \(\cap\) B = (1; m - 1), tập nghiệm của hệ là (1; m - 1)
Nếu m - 1 ≥ 4 tức m ≥ 5 thì A \(\subset\) B. Tập nghiệm của hệ là A = (1; 4)

\(\left(m-2\right)x^4-2\left(m+1\right)x^2+2m-1=0\left(1\right)\)
\(m=2\left(ktm\right)\)
\(m\ne2:đặt:x^2=t\ge0\Rightarrow\left(1\right)\Leftrightarrow\left(m-2\right)t^2-2\left(m+1\right)t+2m-1=0\)
\(3nghiem\Leftrightarrow\left\{{}\begin{matrix}2m-1=0\\t1+t2=\dfrac{2m+2}{m-2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m\in\phi\)
\(4nghiem\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\t1+t2>0\Leftrightarrow\\t1.t2>0\end{matrix}\right.\left\{{}\begin{matrix}\left(m+1\right)^2-\left(m-2\right)\left(2m-1\right)>0\\\dfrac{2m+2}{m-2}>0\\\dfrac{2m-1}{m-2}>0\end{matrix}\right.\)
giải hệ bất pt trên=>m
\(c3:b;\left\{{}\begin{matrix}-8\le x\le-2\\m\left(x-3\right)\ge1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-8\le x\le-2\\m\le\dfrac{1}{x-3}\end{matrix}\right.\)
\(có\) \(nghiệm\Leftrightarrow m\le max:\dfrac{1}{x-3}trên\left[-8;-2\right]\)
\(\Leftrightarrow m\le\dfrac{-1}{5}\)
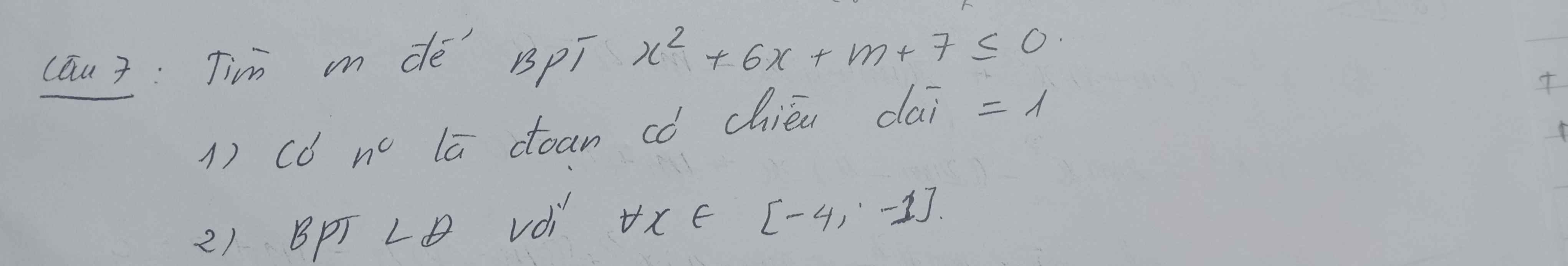

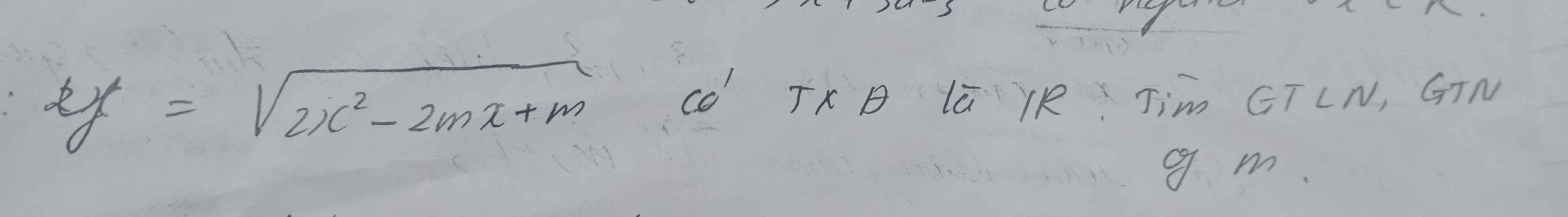




a. Gọi \(x_1>x_2\) là 2 nghiệm của \(x^2+6x+m+7=0\) thì BPT đã cho có tập nghiệm là đoạn có chiều dài bằng 1 khi và chỉ khi \(x_1-x_2=1\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=1\)
\(\Leftrightarrow36-4\left(m+7\right)=1\)
\(\Leftrightarrow m=\dfrac{7}{4}\)
b. \(x^2+6x+m+7\le0\) ;\(\forall x\in\left[-4;-1\right]\)
\(\Leftrightarrow x^2+6x+7\le-m\) ; \(\forall x\in\left[-4;-1\right]\)
\(\Leftrightarrow-m\ge\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)\)
Xét hàm \(f\left(x\right)=x^2+6x+7\) trên \(\left[-4;-1\right]\)
\(-\dfrac{b}{2a}=-3\in\left[-4;-1\right]\) ; \(f\left(-4\right)=-1\) ; \(f\left(-3\right)=-2\) ; \(f\left(-1\right)=2\)
\(\Rightarrow\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)=2\Rightarrow-m\ge2\)
\(\Rightarrow m\le-2\)