
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-2\right)^5-\left(x-2\right)^3=0\)
\(\Rightarrow\left(x-2\right)^3\left(\left(x-2\right)^2-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\\left(x-2\right)^2-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\\left(x-2\right)^2=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x-2=1\\x-2=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=3\\x=1\end{matrix}\right.\)
Vậy \(x\in\left\{1;2;3\right\}\)
⇒ ( x - 2)3 . (x - 2)2 - (x - 2)3 . 1 = 0 ⇒ ( x - 2)3 . [( x - 2)2 - 1] = 0

\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}=\frac{1}{2.2}+\frac{1}{3.3}+\frac{1}{4.4}+...+\frac{1}{100.100}\)
\(< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{99.100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}< 1\)(ĐPCM)

Bài 10:
$-A=\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}$
$=\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{9.10}$
$=\frac{5-4}{4.5}+\frac{6-5}{5.6}+\frac{7-6}{6.7}+...+\frac{10-9}{9.10}$
$=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+....+\frac{1}{9}-\frac{1}{10}$
$=\frac{1}{4}-\frac{1}{10}=\frac{3}{20}$
$\Rightarrow A=\frac{-3}{20}$
Bài 11:
$A=\frac{2n}{n+3}=\frac{2(n+3)-6}{n+3}=2-\frac{6}{n+3}$
Để $A$ nguyên thì $\frac{6}{n+3}$ nguyên.
Với $n$ nguyên thì điều trên xảy ra khi $6\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 2; \pm 3; \pm 6\right\}$
$\Rightarrow n\in\left\{-4; -2; -1; -5; -6; 0; -9; 3\right\}$


\(\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{13.15}\right).x=\dfrac{-26}{45}\\ \Leftrightarrow\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{13.15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{13}-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\dfrac{14}{15}.x=\dfrac{-52}{45}\\ \Leftrightarrow x=-\dfrac{26}{21}\)
(11.3+13.5+...+113.15).x=−2645⇔(21.3+23.5+...+213.15).x=−5245⇔(1−13+13−15+...+113−115).x=−5245⇔(1−115).x=−5245⇔1415.x=−5245⇔x=−2621

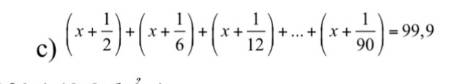

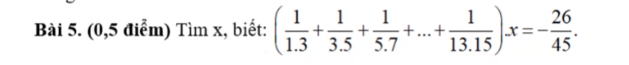
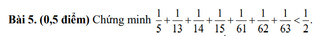
=>x+1/2+x+1/6+...+x+1/90=99,9
=>\(\left(x+x+...+x\right)+\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{90}\right)=99.9\)
=>\(9x+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)=99.9\)
=>9x+(1-0,1)=99,9
=>9x=99,9+0,1-1=100-1=99
=>x=11