Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(a^2\cdot a^3\cdot a^7\cdot b^2\cdot b\)
\(=\left(a^2\cdot a^3\cdot a^7\right)\cdot\left(b^2\cdot b\right)\)
\(=a^{12}\cdot b^3\)
b) \(b^6\cdot b\cdot c^7\cdot c^8\)
\(=\left(b^6\cdot b\right)\cdot\left(c^7\cdot c^8\right)\)
\(=b^7\cdot c^{15}\)
c) \(a^8\cdot a^9\cdot a\cdot c\cdot c^{20}\)
\(=\left(a^8\cdot a^9\cdot a\right)\cdot\left(c\cdot c^{20}\right)\)
\(=a^{18}\cdot c^{21}\)
d) \(a^2\cdot a^3\cdot b^4\cdot c\cdot c^3\)
\(=\left(a^2\cdot a^3\right)\cdot b^4\cdot\left(c\cdot c^3\right)\)
\(=a^5\cdot b^4\cdot c^4\)
a) Kiểm tra lại nhé
b) \(b^6.b^7.c^8\)
\(=b^{6+7}.c^8=b^{13}.c^8\)
c) \(a^8.a^9.a.c.c^{20}\)
\(=a^{8+9+1}.c^{1+20}\)
\(=a^{18}.c^{21}\)
d) \(a^2.a^3.b^4.c.c^3\)
\(=a^{2+3}.b^4.c^{1+3}\)
\(=a^5.b^4.c^4\)
\(#WendyDang\)

\(a,\left(-5\right).\left|x\right|=-75\)
\(\left|x\right|=\frac{-75}{-5}=15\)
\(\Rightarrow\orbr{\begin{cases}x=15\\x=-15\end{cases}}\)
Vậy....
\(b,\left(-6\right)^3.x^2=-1944\)
\(-216.x^2=-1944\)
\(x^2=9\)
\(\Rightarrow x=\pm3\)
Vậy....
\(d,\left|9-x\right|=-7+64\)
\(\left|9-x\right|=57\)
\(\Rightarrow\orbr{\begin{cases}9-x=57\\9-x=-57\end{cases}\Rightarrow\orbr{\begin{cases}x=-48\\x=66\end{cases}}}\)
Vậy...
\(e,\left|x+101\right|-\left(-16\right)=\left(-43\right).\left(-5\right)\)
\(\left|x+101\right|+16=215\)
\(\left|x+101\right|=199\)
\(\Rightarrow\orbr{\begin{cases}x+101=199\\x+101=-199\end{cases}\Rightarrow\orbr{\begin{cases}x=98\\x=-300\end{cases}}}\)
Vậy..
hok tốt!!
a,\(\left(-5\right).\left|x\right|=-75\)
\(=>\left|x\right|=-75:\left(-5\right)=15\)
\(=>\orbr{\begin{cases}x=15\\x=-15\end{cases}}\)
b,\(\left(-6\right)^3.x^2=-1944\)
\(=>\frac{1944}{216}=x^2\)
\(=>x=\sqrt{\frac{1944}{216}}=3\)


1. 2x=16\(\Rightarrow\)X=4
2. 22x-1=27
\(\Rightarrow\)27=22.4-1
Vậy x =4

`(2^x+1)^2 =25`
`=> (2^x+1)^2 = (+-5)^2`
\(\Rightarrow\left[{}\begin{matrix}2^x+1=5\\2^x+1=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2^x=4\\2^x=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)
\(\left(x+6\right)\left(5^x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\5^x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\5^x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=0\end{matrix}\right.\)
\(\left(x-3\right)^{2023}=x-3\)
\(\Rightarrow\left(x-3\right)^{2023}-\left(x-3\right)=0\)
\(\Rightarrow\left(x-3\right)\left[\left(x-3\right)^{2022}-1\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\\left(x-3\right)^{2022}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x-3=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)

1. a) 4.415.8.25.125
= (4.25). (8.125).415
= 100.1000.415
= 100000.415
= 41500000
b) 2.31.12+4.42.6+8.27.3
= (2.31.12)+(4.42.6)+(8.27.3)
= (2.12).31+(4.6).42+(8.3).27
= 24.31+24.42+24.27
= 24 (31+42+27)
= 24.100
= 2400
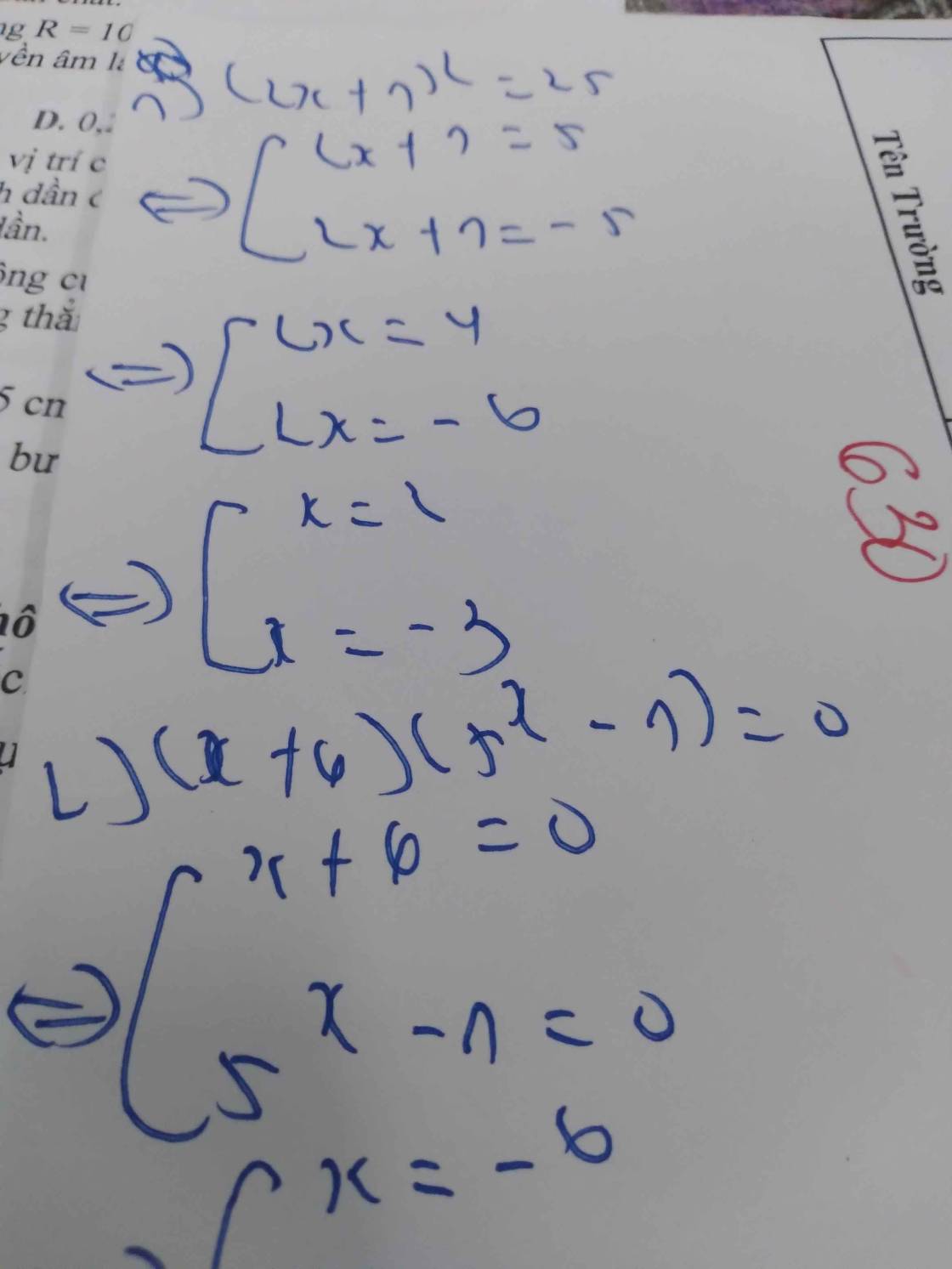


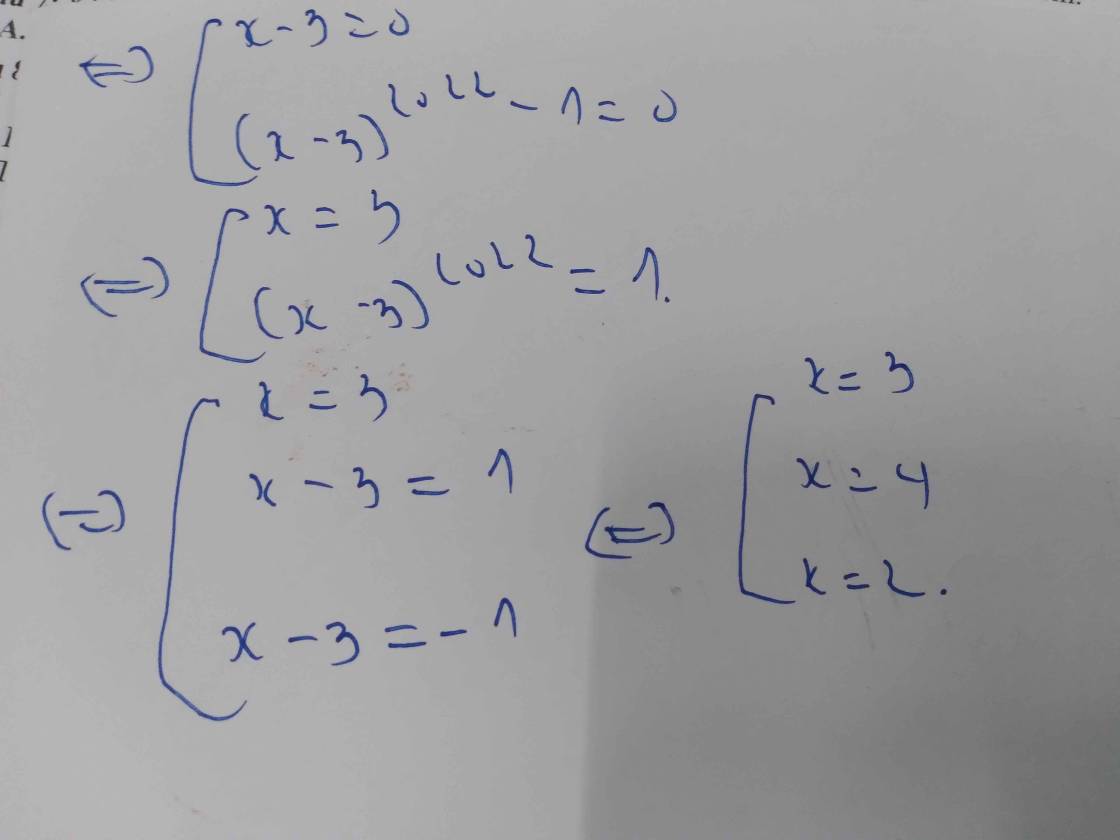
1, 15-(2x-3)=6
<=>2x-3=15-6
<=>2x=15-6+3
<=>2x=12
<=>x=12:2
<=>x=6
Vậy x=6
2, (x-2).3=3\(^2\)
<=>x-2=3\(^2\):3
<=>x-2=9:3
<=>x=9:3-2
<=>x=1
vậy x=1
3, (x+7)-25=13
<=>x+7=13+25
<=>x=13+25-7
<=>x=31
Vậy x=31
4, 450:(x-190)=50
<=>x-190=450:50
<=>x=450:50+/ 190
<=>x=199
Vậy x=199
5, 3 \(^x\)x 2=18
<=>3\(^x\)=18:2
<=>3\(^x\)=9=3\(^2\)
=>x=2
vậy x=2