K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
1
AH
Akai Haruma
Giáo viên
4 tháng 1 2017
Biến đổi:
\(8B=8xyz[(xy+yz+xz)(x+y+z)-xyz]=8xyz(xy+yz+xz-xyz)\)
Áp dụng BĐT Am-Gm dạng \(ab\leq\left(\frac{a+b}{2}\right)^2\Rightarrow 8B\leq\left(\frac{xy+yz+xz+7xyz}{2}\right)^2\)
Bằng Am-Gm dễ dàng chứng minh \(xy+yz+xz\leq\frac{(x+y+z)^2}{3}=\frac{1}{3};xyz\leq\frac{1}{27}\)
Do đó: \(8B\leq\frac{64}{729}\Rightarrow B_{max}=\frac{8}{729}\) \(\Rightarrow 9^3k=\frac{8}{729}.9^3=8\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
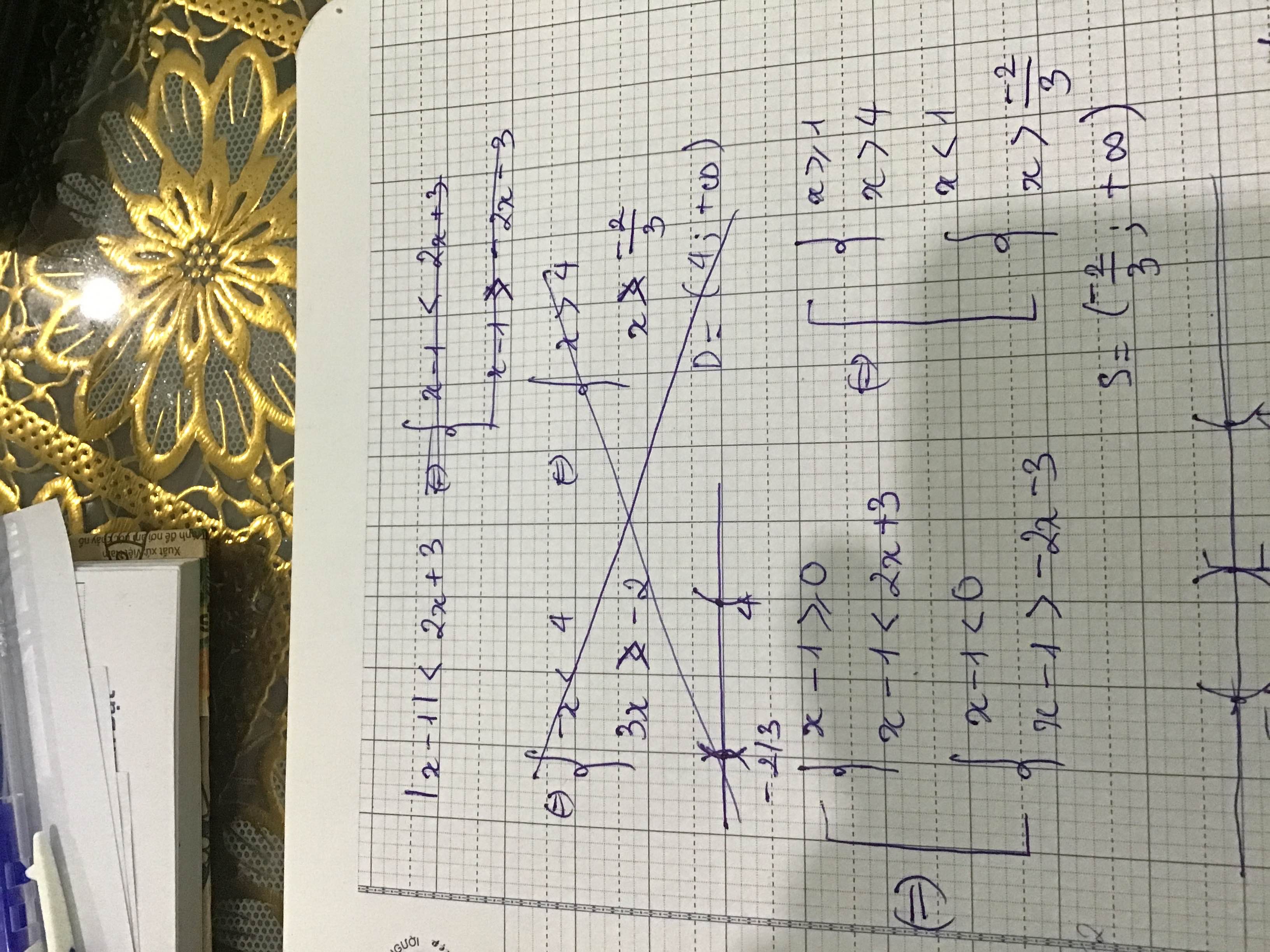
Ngoại trừ nhầm lẫn 1 chút xíu ở chỗ lẽ ra là \(x>-4\) thì em ghi thành \(x>4\), còn lại thì đúng
Kết luận nghiệm cũng đúng rồi.
Hợp nghiệm của ngoặc nhọn thì lấy giao các tập nghiệm, hợp nghiệm của ngoặc vuông thì lấy hợp các tập nghiệm
23 tháng 8 2021
a)TXĐ:\(D=R\)
b)\(f\left(\dfrac{2}{3}\right)=\left(\dfrac{2}{3}\right)^2+\dfrac{2}{3}-2=-\dfrac{8}{9}\)
\(f\left(3\right)=3-2.3=-3\)
KA
1
\(\left|1-2x\right|< 5-x\)
\(\Leftrightarrow-\left(5-x\right)< 1-2x< 5-x\)
\(\Leftrightarrow x-5< 1-2x< 5-x\)
\(\Leftrightarrow-4< x< 2\)
Ta có : | 1 − 2 x | < 5 − x
=> − ( 5 − x ) < 1 − 2 x < 5 − x
=> x − 5 < 1 − 2 x < 5 − x
=> − 4 < x < 2