Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

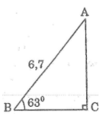
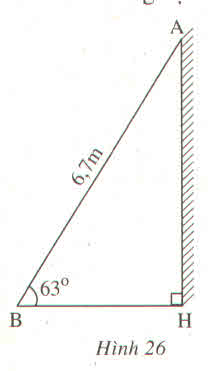
Chiều cao của thang là cạnh góc vuông đối diện với góc 63 °
Ta có: AC = AB.sinB = 6,7.sin 63 ° ≈ 6 (m)
Vậy chiều cao của cái thang đạt được so với mặt đất là 6m.

Không nhầm thì Sin62°×4=3.53m
hình như thế, k bt đúng k ạ :>>
chúc bn học tốt

Sửa đề: AB=3cm; AC=4cm; BH=1,8cm
a: Xét ΔABC vuông tại A có AH là đường cao
nên \(BA^2=BH\cdot BC\)
=>BC=3^2/1,8=5(cm)
ΔABC vuông tại A có AH là đường cao
nên CA^2=CH*CB
=>CH*5=4^2=16
=>CH=3,2(cm)
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>AH^2=3^2-1,8^2=5,76
=>AH=2,4(cm)
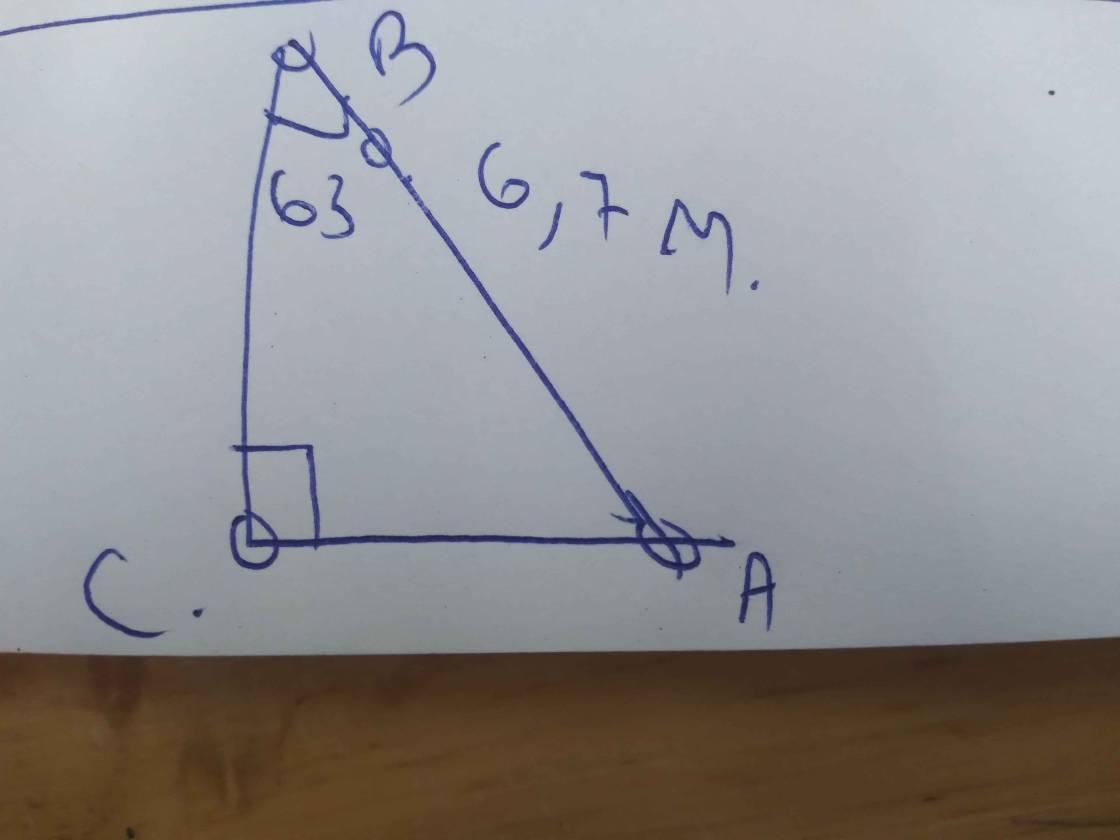
b: góc tạo bởi thang với tường là:
90-63=27 độ
Chiều cao của thang so với mặt đất là:
\(7\cdot sin27\simeq3,18\left(cm\right)\)

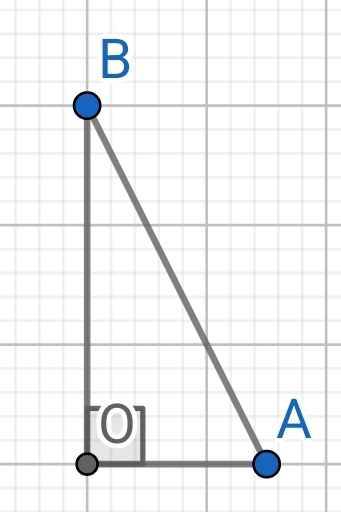 Thang chạm tường ở điểm B như trên hình.
Thang chạm tường ở điểm B như trên hình.
⇒ OB là độ cao cần tính
Ta có:
sin A = OB/AB
⇒ OB = AB . sin A
= 5 . sin 65⁰
≈ 4,5 (m)
Theo đề bài : \(l=5\left(m\right);\alpha=65^o\) (\(\alpha\) là góc tạo bởi chân thang và mặt đất)
Thang chạm tường ở độ cao \(h\) so với mặt đất là :
\(sin\alpha=\dfrac{h}{l}\Rightarrow h=l.sin\alpha=5.sin65^o\sim4,5\left(m\right)\)

Gọi độ dài của thang là BC, khoảng cách từ chân thang đến chân tường là AC
Theo đề, ta có: BC=3,5m; AC=1,6m; AC\(\perp\)AB tại A
Ta có: ΔABC vuông tại A
=>\(cosC=\dfrac{CA}{CB}\)
=>\(cosC=\dfrac{1.6}{3.5}=\dfrac{16}{35}\)
=>\(\widehat{C}\simeq63^0\)
=>\(60^0< =\widehat{C}< =65^0\)
=>Đạt tiêu chuẩn