Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Gọi xác suất của trong 5 người được chọn có ít nhất 3 thầy cô là P(A)
cách chọn 1 cô,4 thầy : \(5.C^4_7\)
cách chọn 2 cô, 3 thầy \(C\overset{2}{5}.C^3_7\)
=> \(P\left(\overline{A}\right)=\dfrac{5.C^4_7+C^2_5.C^3_7}{C^5_{12}}=\dfrac{175}{264}\)
=> P(A)= 1-\(\dfrac{175}{264}=\dfrac{89}{264}\)

Đáp án B
Ta có: chọn ra 4 thầy cô từ 16 thầy cô có ![]() (cách chọn)
(cách chọn)
+ Để chọn được 4 giáo viên phải có cô giáo và đủ ba bộ môn, vậy có các trường hợp sau:
* Trường hợp 1: chọn 2 thầy toán, 1 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 2: chọn 1 thầy toán, 2 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 3: chọn 1 thầy toán, 1 cô lý, 2 cô hóa có ![]() (cách chọn)
(cách chọn)
Vậy xác suất để chọn được 4 người phải có cô giáo và có đủ ba bộ môn là
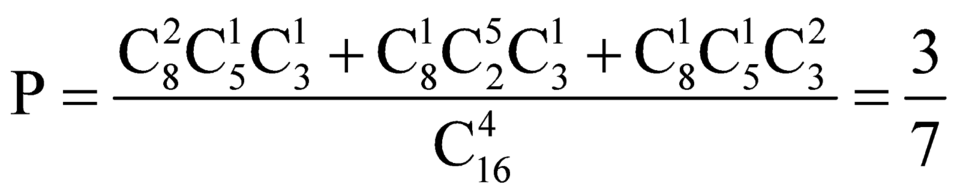

Chọn C
Gọi biến cố A: “2 giáo viên tập huấn gồm 1 thầy giáo và 1 cô giáo”.
Suy ra ![]() .
.
Vậy 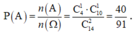 .
.

Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có ![]() cách.
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có ![]() cách.
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 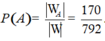
Chọn C.

http://www.toanhocnhatrang.com/2015/05/bai-toan-so-298.html
Gọi A là tập hợp cách chọn đề có 3 câu dễ, 1 câu khó, 1 câu trung bình.
B là tập hợp cách chọn đề có 2 câu dễ, 2 câu khó, 1 câu trung bình
C là tập hợp cách chọn đề có 2 câu dễ, 1 câu khó, 2 câu trung bình
D là tập hợp cách chọn đề thỏa mãn yêu cầu đề ra. Ta có:
D = A \(\cup\) B \(\cup\) C
ngoài ra A,B,C đôi một không giao nhau. Theo quy tắc cộng ta có
\(\left|D\right|\) = \(\left|A\right|\) + \(\left|B\right|\) + \(\left|C\right|\) (1)
Theo quy tắc nhân ta có
\(\left|A\right|\) = \(C_{15}^3\).\(C_5^1\).\(C_{10}^1\) = 22750
\(\left|B\right|\) = \(C_{15}^2\).\(C_5^2\).\(C_{10}^1\) = 10500
\(\left|C\right|\) = \(C_{15}^2\).\(C_5^1\).\(C_{10}^2\) = 23625
Thay vào (1) ta có \(\left|D\right|\) = 56875
Vậy có 56875 cách chọn đề kiểm tra.

Đáp án D.
Sô cách lấy bằng số cách chọn ra 6 quyển để bỏ lại. Yêu cầu đặt ra là 6 quyển để lại phải đủ cả 3 môn.
TH1: 1 văn, 2 âm nhạc, 3 hội họa: C 5 1 . C 4 2 . C 3 3
TH2: 1 văn, 3 âm nhạc, 2 hội họa: C 5 1 . C 4 3 . C 3 2
TH3: 1 văn, 4 âm nhạc, 1 hội họa: C 5 1 . C 4 4 . C 3 1
TH4: 2 văn, 1 âm nhạc, 3 hội họa: C 5 2 . C 4 1 . C 3 3
TH5: 2 văn, 2 âm nhạc, 2 hội họa: C 5 2 . C 4 2 . C 3 2
TH6: 2 văn, 3 âm nhạc, 1 hội họa: C 5 2 . C 4 3 . C 3 1
TH7: 3 văn, 1 âm nhạc, 2 hội họa: C 5 3 . C 4 1 . C 3 2
TH8: 3 văn, 2 âm nhạc, 1 hội họa: C 5 3 . C 4 2 . C 3 1
TH9: 4 văn, 1 âm nhạc, 1 hội họa: C 5 4 . C 4 1 . C 3 1
Lấy 6 quyển sách chia cho 6 bạn: 6! = 720
Nhân lại ta có : 579600 cách

Ta đi tìm số cách chọn ra 5 bạn mà trong đó có cả hai bạn Thùy và Thiện.
Bước 1: Chọn nhóm 3 em trong 13 em, trừ Thùy và Thiện thì có ![]() cách.
cách.
Bước 2: Ghép 2 em Thùy và Thiện có 1 cách.
Vậy theo quy tắc nhân thì có 286 cách chọn 5 em trong đó cả Thùy hoặc Thiện đều được chọn.
- Chọn 5 em bất kì trong số 15 em có ![]() cách. Vậy theo yêu cầu đề bài thì có tất cả 3003-286=2717 cách chọn mà trong đó có ít nhất một trong hai em Thùy và Thiện không được chọn.
cách. Vậy theo yêu cầu đề bài thì có tất cả 3003-286=2717 cách chọn mà trong đó có ít nhất một trong hai em Thùy và Thiện không được chọn.
Chọn C.
TH1. hội đồng gồm 3 thầy, 2 cô trong đó có thầy An nhưng không có cô Bình.
Khi đó ta cần chọn 2 trong 6 thầy còn lại (trừ thầy An) rồi chọn 2 trong 4 cô (trừ cô Bình)
Có C 6 2 . C 4 2 = 60
TH2. hội đồng gồm 3 thầy, 2 cô trong đó có cô Bình nhưng không có thầy An.
Khi đó ta cần chọn 3 trong 6 thầy còn lại (trừ thầy An) rồi chọn 1 trong 4 cô (trừ cô Bình)
Có C 6 3 . C 4 1 = 80
Vậy, có 60+80=140 cách lập hội đồng coi thi.
Chọn A.