Tham khảo:

\(S_{max}=m\cdot2A+2Asin\dfrac{\Delta\varphi}{2}\Leftrightarrow12=1\cdot2\cdot4+4\)

\(\Rightarrow\left\{{}\begin{matrix}m=1\\\Delta\varphi=\dfrac{\pi}{3}\left(rad\right)\Rightarrow\Delta t=\dfrac{\Delta\varphi}{\dfrac{2\pi}{T}}=\dfrac{\dfrac{\pi}{3}}{\dfrac{2\pi}{T}}=\dfrac{T}{6}\end{matrix}\right.\)

Ta có: \(t=m\dfrac{T}{2}+\Delta t\Leftrightarrow2=1\cdot\dfrac{T}{2}+\dfrac{T}{6}\Rightarrow T=3\left(s\right)\)

Quãng đường mà vật đi được trong một chu kì S = 4A → A = 4 cm

Đáp án B

Đáp án C.

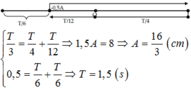
Ta có 

Do  t 1 + t 2 = T / 2  nên quãng đường vật đã đi được sau tổng thời gian này là  S 1 + S 2 = 2 A

Mặt khác  S 1 : S 2 = 1 : 3  nên  S 1 = A / 2  và  S 2 = 3 A / 2 .

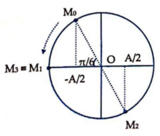
Kết hợp với điều kiện lúc đầu vật không ở vị trí biên nên nếu biểu diễn trên vòng tròn lượng giác của li độ x ta có thể lựa chọn vị trí lúc đầu của vật tương ứng với điểm M₀. Sau các thời gian t₁, t₂ và t₃ tiếp theo, vật ở các vị trí ứng với các điểm M₁, M₂ và  M 1 ≡ M 2 trên vòng tròn lượng giác (hình vẽ bên)

Như vậy, quãng đường vật đi được trong thời gian t₁ là S₁ = A/2, quãng đường vật đi được trong thời gian t₂ là S₂ = A + A/2 = 3A/2 và trong thời gian t₃ là   S₃ = 2A + A/2 = 5A/2

Từ đó suy ra 

Vậy k = 5.

B

+ Quãng đường vật đi được trong nửa chu kì là S = 2A = 18 cm, vậy A = 9 cm.

Đáp án C

phải nói T = bn giây thì mới tính đc chứ :v

khí hidro (H2)

Chọn đáp án B