Nhat_Minh.docx

Bạn vào đây nha có đầy đủ hết

Chúc bn hok tốt!!!

Mk thíu bạn vào thống kê hỏi đáp của mk để lấy link nhoa!!!

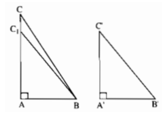
Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′. Ta có tam giác vuông ABC1 bằng tam giác vuông A'B'C', suy ra B′C′=BC1. Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1. Vì AC > AC1 nên BC > BC1. Suy ra BC > B'C'.

MAI VŨ XUÂN MY:

a) Xét tam giác ABD và tam giác EBD có:

                      góc A = góc E ( =90độ)                        

                          BD = BD (Cạnh chung)

                     góc B1=-góc B2 (phân giác)

    Vậy tam giác ABD = tam giác EBD (chgn)

b) Ta có: tam giác ABD = tam giác EBD (cm a)

=> AB = AE (cạnh tương ứng)

=> tam giác ABE cân tại B  

Mà góc B = 60 độ

=> góc A = góc E = \(\frac{180^0-60^0}{2}\)=60 độ

Vậy tam giác ABE là tam giác đều

c) BC=7cm

bai 84,85,86,87 sbt trang 149 lop 7 

giai ho mk voi

Theo định lý Pytago, tam giác ABC ( Góc A=90 độ ) có:

\(BC^2=AB^2+AC^2\)

Mà AB, BC, AC > 0 nên BC² > AB², BC² > AC² hay BC > AB và AC suy ra BC lớn nhất

a: Do AC > A'C' nên lấy được điểm C₁ trên cạnh AC sao cho AC₁=A′C′.

Ta có  ΔABC₁=ΔA'B'C'

Suy ra B′C′=BC1

Mặt khác hai đường xiên BC và BC₁ kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC₁.

Vì AC > AC1 nên BC > BC1.

Suy ra BC > B'C'.

b: 

-Giả sử AC<A'C'.

Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.

Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).

Suy ra BC=B'C'.

Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.

Định lí Pitago (Thuận): Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông.

Vẽ hình:

Tam giác ABC vuông tại A

=> BC² = AB² + AC²