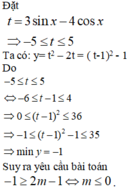Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x^3-x^2(m+3)+x(3m+2)-2m=0
=>(x-1)(x^2-(m+2)x+2m)=0
=>x=1 hoặc x^2-(m+2)x+2m=0
Để PT có 3 nghiệm thì (m+2)^2-4*2m>0 và 1^2-(m+2)+2m<>0
=>m<>1 và m<>2
=>x2=(m+2-m+2)/2=2 và x3=(m+2+m-2)/2=m
Để tạo thành cấp sô nhân thì
x1<x2<m hoặc m<x1<x2 hoặc x1<m<x2
=>m*1=2^2 hoặc 2m=1 hoặc m^2=2
=>m=4 hoặc m=1/2 hoặc m=căn 2

Câu 1:
Đặt \(f\left(x\right)=x^3+mx^2+\left(m-3\right)x-1\)
Ta có \(f\left(0\right)=-1\) ; \(f\left(-1\right)=1\)
\(\Rightarrow f\left(0\right).f\left(-1\right)< 0\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
Mặt khác \(\left\{{}\begin{matrix}f\left(0\right)=-1< 0\\\lim\limits_{x\rightarrow+\infty}=+\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;+\infty\right)\)
\(\left\{{}\begin{matrix}f\left(-1\right)=1>0\\\lim\limits_{x\rightarrow-\infty}=-\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-\infty;-1\right)\)
Vậy pt đã cho có 3 nghiệm phân biệt với mọi m
Câu 2:
\(f'\left(x\right)=x^2+2\left(m-1\right)x+m+1\)
Để \(f'\left(x\right)\ge0\) \(\forall x\) \(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m+1\right)\le0\)
\(\Leftrightarrow m^2-3m\le0\Leftrightarrow0\le m\le3\)
Câu 3:
Nhận thấy \(x=0\) không phải nghiệm
\(\Leftrightarrow2x^3+3x^2-2=-mx\)
\(\Leftrightarrow\frac{2x^3+3x^2-2}{x}=-m\)
Đặt \(f\left(x\right)=\frac{2x^3+3x^2-2}{x}\Rightarrow f'\left(x\right)=\frac{\left(6x^2+6x\right)x-\left(2x^3+3x^2-2\right)}{x^2}=\frac{4x^3+3x^2+2}{x^2}\)
\(f'\left(x\right)=\frac{4x^2\left(x+1\right)+2-x^2}{x^2}\Rightarrow f'\left(x\right)>0\) \(\forall x\in\left(-1;1\right)\)
\(\Rightarrow f\left(x\right)\) đồng biến trên \(\left(-1;1\right)\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=+\infty\) ; \(\lim\limits_{x\rightarrow0^+}f\left(x\right)=-\infty\)
\(\Rightarrow y=-m\) luôn cắt đồ thị \(y=f\left(x\right)\) hay phương trình đã cho luôn có ít nhất 1 nghiệm trong khoảng \(\left(-1;1\right)\) với mọi m

ĐKXĐ: \(cosx\ne\frac{3}{4}\)
\(\Leftrightarrow3sinx+m=8cosx-6\)
\(\Leftrightarrow3sinx-8cosx=-m-6\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(3^2+8^2\ge\left(-m-6\right)^2\)
\(\Rightarrow\left(m+6\right)^2\le73\)
\(\Rightarrow-6-\sqrt{73}\le m\le-6+\sqrt{73}\)
Kết hợp thêm điều kiện \(m\ne12\pm\frac{3\sqrt{7}}{4}\)

Lời giải:
Đặt \(3\sin x+4\cos x=t\)
Áp dụng BĐT Bunhiacopxky:
\(t^2=(3\sin x+4\cos x)^2\leq (3^2+4^2)(\sin ^2x+\cos ^2x)=25\)
\(\Rightarrow -5\leq t\leq 5\)
Với $t\in [-5;5]$ ta có:
\(y=3t^2+4t+1\leq 3.25+4.5+1=96\)
Mặt khác: \(y=3t^2+4t+1=3(t+\frac{2}{3})^2-\frac{1}{3}\)
\((t+\frac{2}{3})^2\geq 0, \forall t\in [-5;5]\Rightarrow y\geq -\frac{1}{3}\)
Vậy \(y_{\min}=\frac{-1}{3}; y_{\max}=96\)

Đáp án D
Đặt t = 3sin x - 4cos x => -5 ≤ t ≤ 5 (dùng bất đẳng thức bunhiacopxki)
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 2)2 -1
Do -5 ≤ t ≤ 5 => 0 ≤ (t – 2)2 ≤ 36 => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.

Đặt \(t=3sinx-4cosx=5\left(\frac{3}{5}sinx-\frac{4}{5}cosx\right)=5sin\left(x-a\right)\)
\(\Rightarrow-5\le t\le5\)
\(\Rightarrow y=t^2-t+m\)
\(y>0\) ; \(\forall m\Leftrightarrow t^2-t+m>0\Leftrightarrow m>-t^2+t\) ; \(\forall m\)
\(\Leftrightarrow m>\max\limits_{\left[-5;5\right]}\left(-t^2+t\right)\)
Mà \(-t^2+t=-\left(t-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
\(\Rightarrow m>\frac{1}{4}\)

ĐKXĐ; ...
\(\Leftrightarrow\frac{3}{5}sinx+\frac{4}{5}cosx-1=\frac{1}{5}\left(4tanx-3\right)^2\)
\(\Leftrightarrow sin\left(x+a\right)-1=\frac{1}{5}\left(4tanx-3\right)^2\)
(Trong đó \(a\in\left(0;\pi\right)\) sao cho \(cosa=\frac{3}{5}\))
Do \(\left\{{}\begin{matrix}sin\left(x+a\right)-1\le0\\\left(4tanx-3\right)^2\ge0\end{matrix}\right.\) \(\forall a;x\) nên đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}sin\left(x+a\right)=1\\4tanx-3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3sinx+4cosx=5\\4sinx-3cosx=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}sinx=\frac{3}{5}\\cosx=\frac{4}{5}\end{matrix}\right.\) \(\Rightarrow x=arcsin\left(\frac{3}{5}\right)+k2\pi\)