Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

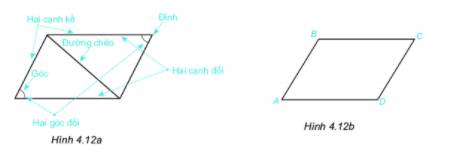
1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.

- Đo góc, ta được góc ở đỉnh H của hình thang cân EFGH bằng góc G.
- Các cạnh bên của hình thang cân là EH và FG nên EH = FG (tính chất hình thang cân).
Các đường chéo là EG và FH nên EG = FH (tính chất hình thang cân).

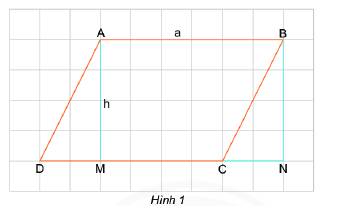
\(\begin{array}{l}{S_{AMD}} = \frac{{h.MD}}{2};{S_{BNC}} = \frac{{h.NC}}{2};MD = NC\\ \Rightarrow {S_{AMD}} = {S_{BNC}}\end{array}\)
Vậy diện tích tam giác AMD bằng diện tích tam giác BNC.
- Diện tích hình bình hành ABCD tổng diện tích AMD và diện tích ABCM.
- Diện tích hình chữ nhật ABNM bằng tổng diện tích BNC và diện tích ABCM.
Từ (1),(2) và (3) ta được, diện tích hình bình hành ABCD bằng diện tích hình chữ nhật ABNM.

Ta có: AB= 5/2 AD
mà AB + AD = 70/2 =35 (cm)
=> 5/2AD + AD = 35
5/2AD + 2/2AD = 35.2/2 = 70/2
7/2AD = 70/2
=> AD = 70/2.2/7
=> AD = 10 (cm)
=> AB = 35 - 10 = 25 (cm)
=> Diện tích hình bình hành ABCD là:
25.9 = 225 (cm2)
Vậy diện tích hình bình hành là 225 (cm2)

Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)

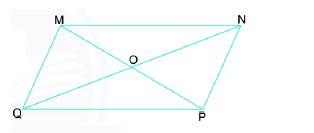

Hình bình hành MNPQ có:
- Các góc đối bằng nhau nên góc đỉnh M của hình bình hành MNPQ bằng góc đỉnh P
- Điểm O là trung điểm của MP nên OM=OP (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Điểm O là trung điểm của NQ nên ON=OQ (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).