Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

EFGH là hình thang cân
=>EH=GF và HF=EG
=>FG=4cm và EG=7cm

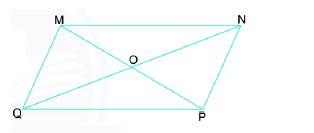
Hình bình hành MNPQ có:
- Các góc đối bằng nhau nên góc đỉnh M của hình bình hành MNPQ bằng góc đỉnh P
- Điểm O là trung điểm của MP nên OM=OP (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Điểm O là trung điểm của NQ nên ON=OQ (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).

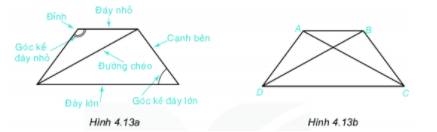
1) Đỉnh: A, B, C, D
Đáy lớn: DC
Đáy nhỏ: AB
Đường chéo: AC, BD
Cạnh bên AD, BC
2) Dùng thước thẳng hoặc compa, ta đo được: AD = BC; AC = BD
Vậy: Hai cạnh bên hình thang cân bằng nhau
Hai đường chéo hình thang cân bằng nhau.
3) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
Vậy hai đáy của hình thang cân song song với nhau.
4) Hai góc kề một đáy của hình thang bằng nhau.

Hình thang cân trong các hình thang là : HKIJ (vì có HJ = IK)

Các phát biểu sau đây khẳng định nào đúng?
A. Hình chữ nhật có 4 góc bằng nhau và bằng 900
B. Hình thoi có 4 góc bằng nhau và bằng 900. 4 cạnh bằng nhau
C. Hình thang cân có hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau
D. Hình lục giác đều có 4 góc bằng nhau và 6 cạnh bằng nhau

- Đo góc, ta được góc ở đỉnh H của hình thang cân EFGH bằng góc G.
- Các cạnh bên của hình thang cân là EH và FG nên EH = FG (tính chất hình thang cân).
Các đường chéo là EG và FH nên EG = FH (tính chất hình thang cân).