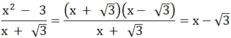
ĐKXĐ: `x>=0;x\ne9`

`(x^2-3)/(sqrtx-3)=((x-sqrt3)(x+sqrt3))/(x+sqrt3)=x-sqrt3`

`a)(x^2-3)/(x+\sqrt3)`

`->` ĐKXĐ : `x>=0;x\ne9`

`=((x-\sqrt3)(x+\sqrt3))/(x+\sqrt3)`

`=(x-\sqrt3)/1`

`=x-\sqrt3`

1: ĐKXĐ: \(a\ge0\)

a) Ta có: \(A=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}-\dfrac{3x+3}{x-9}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)

\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{1}{\sqrt{x}+1}\)

\(=\dfrac{-3}{\sqrt{x}+3}\)

b) Ta có: \(x=\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\)

\(=\sqrt{2}+1-\sqrt{2}+1\)

=2

Thay x=2 vào A, ta được:

\(A=\dfrac{-3}{3+\sqrt{2}}=\dfrac{-9+3\sqrt{2}}{7}\)

tách mẫu hạng tử thứ nhất rồi quy đồng

cíuuu

a: =căn 3+căn 5-căn 3=căn5
b: \(=\sqrt{x-2-2\sqrt{x-2}+1}=\sqrt{\left(\sqrt{x-2}-1\right)^2}\)

\(=\left|\sqrt{x-2}-1\right|\)

Ta có: \(\left(\sqrt{12}-2\sqrt{18}+5\sqrt{3}\right)\cdot\sqrt{3}+5\sqrt{6}\)

\(=\left(2\sqrt{3}-6\sqrt{3}+5\sqrt{3}\right)\cdot\sqrt{3}+5\sqrt{6}\)

\(=3+5\sqrt{6}\)

a: \(B=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{x-9}=\dfrac{x+9}{x-9}\)

b: \P=A:B

\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}-3}\cdot\dfrac{x-9}{x+9}=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}{x+9}>=\dfrac{-1\cdot3}{9}=\dfrac{-1}{3}\)

Dấu = xảy ra khi x=0

\(a,=27-5\sqrt{3x}\\ b,=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+28=14\sqrt{2x}+28\)

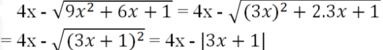
Tại x = -√3 ta được:

= 4(-√3) - |3(-√3) + 1|

= -4√3 - |-3√3 + 1|

= -4√3 - (3√3 - 1)

= -7√3 + 1

a: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)

Ta có: \(B=\dfrac{6-7x}{x^2-4}+\dfrac{3}{x+2}-\dfrac{2}{2-x}\)

\(=\dfrac{6-7x+3x-6+2x+4}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{-2x+4}{\left(x+2\right)\left(x-2\right)}\)

\(=-\dfrac{2}{x+2}\)