K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 7 2021
\(C=\sqrt{\dfrac{x-6\sqrt{x}+9}{x+6\sqrt{x}+9}}=\sqrt{\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+3\right)^2}}=\dfrac{\left|\sqrt{x}-3\right|}{\sqrt{x}+3}\)
Vì \(x\ge9\Rightarrow\sqrt{x}\ge3\Leftrightarrow\sqrt{x}-3\ge0\)
\(\Rightarrow C=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
\(D=\dfrac{x-1}{\sqrt{y}-1}.\sqrt{\dfrac{y-2\sqrt{y}+1}{\left(x-1\right)^4}}\) (\(x;y\ne1;y\ge0\))
\(=\dfrac{x-1}{\sqrt{y}-1}.\dfrac{\sqrt{\left(\sqrt{y}-1\right)^2}}{\left(x-1\right)^2}=\dfrac{\left|\sqrt{y}-1\right|}{\left(\sqrt{y}-1\right)\left(x-1\right)}\)
TH1: \(\sqrt{y}-1>0\Leftrightarrow y>1\)
\(\Rightarrow D=\dfrac{\sqrt{y}-1}{\left(\sqrt{y}-1\right)\left(x-1\right)}=\dfrac{1}{x-1}\)
TH2:\(\sqrt{y}-1< 0\Leftrightarrow0\le y< 1\)
\(\Rightarrow D=\dfrac{-\left(\sqrt{y}-1\right)}{\left(\sqrt{y}-1\right)\left(x-1\right)}=\dfrac{-1}{x-1}\)
Vậy...
\(E=\dfrac{1}{2x-1}.\sqrt{5x^4\left(1-4x+4x^2\right)}\)
\(=\dfrac{1}{2x-1}\sqrt{5x^4\left(2x-1\right)^2}=\dfrac{\sqrt{5}x^2\left|2x-1\right|}{2x-1}\)
TH1: \(2x-1>0\Leftrightarrow x>\dfrac{1}{2}\)
\(\Rightarrow E=\dfrac{\sqrt{5}x^2\left(2x-1\right)}{2x-1}=\sqrt{5}x^2\)
TH2:\(2x-1< 0\Leftrightarrow x< \dfrac{1}{2}\)
\(\Rightarrow E=\dfrac{-\sqrt{5}x^2\left(2x-1\right)}{2x-1}=-\sqrt{5}x^2\)
Vậy...
H
4 tháng 7 2021
c)
\(C=\sqrt{\dfrac{x-6\sqrt{x}+9}{x+6\sqrt{x}+9}}=\sqrt{\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+3\right)^2}}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
d)
\(D=\dfrac{x-1}{\sqrt{y}-1}.\sqrt{\dfrac{y-2\sqrt{y}+1}{\left(x-1\right)^4}}=\dfrac{x-1}{\sqrt{y}-1}.\dfrac{\left|\sqrt{y}-1\right|}{\left(x-1\right)^2}=\dfrac{\left|\sqrt{y}-1\right|}{\left(\sqrt{y}-1\right)\left(x-1\right)}\)
e)
\(E=\dfrac{1}{2x-1}.\sqrt{5x^4\left(1-4x+4x^2\right)}=\dfrac{1}{2x-1}.\sqrt{5x^4.\left(2x-1\right)^2}=\dfrac{1}{2x-1}.\sqrt{5}x^2.\left|2x-1\right|\)
TN
2
19 tháng 8 2021
\(\sqrt{\dfrac{x}{y}}+\sqrt{xy}+\dfrac{x}{y}\sqrt{\dfrac{y}{x}}=\sqrt{\dfrac{x}{y}}+\sqrt{\dfrac{x}{y}}\cdot\sqrt{y^2}+\sqrt{\dfrac{x}{y}}\cdot\sqrt{\dfrac{x}{y}\cdot\dfrac{y}{x}}=\sqrt{\dfrac{x}{y}}\cdot\left(1+y+1\right)=\sqrt{\dfrac{x}{y}}\cdot\left(y+2\right)\)
19 tháng 8 2021
Ta có: \(\sqrt{\dfrac{x}{y}}+\sqrt{xy}+\dfrac{x}{y}\cdot\sqrt{\dfrac{y}{x}}\)
\(=\dfrac{\sqrt{x}}{\sqrt{y}}+\dfrac{\sqrt{x}}{\sqrt{y}}+\sqrt{xy}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{y}}+\dfrac{y\sqrt{x}}{\sqrt{y}}\)
\(=\dfrac{2\sqrt{x}+y\sqrt{x}}{\sqrt{y}}\)
PT
1
PT
1
PT
1
CM
3 tháng 3 2019
3 - 11 2 = 3 - 11 = 11 - 3
(vì √11 - 3 > 0 do 3 = √9 mà √11 > √9)
CM
14 tháng 6 2018
√9a4 + 3a2 = √(3a2)2 + 3a2
= |3a2| + 3a2 = 3a2 + 3a2 = 6a2
(do a2 ≥ 0 với mọi a nên |3a2| = 3a2)
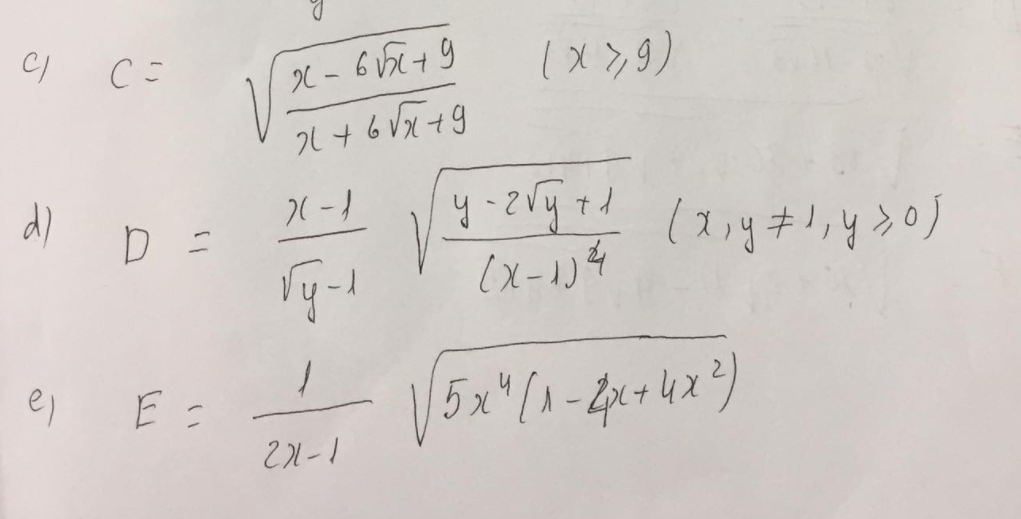
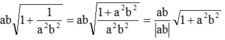
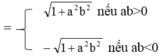
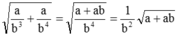
\(1,\dfrac{\sqrt{27\left(x-5\right)^2}}{\sqrt{3}}\left(dkxd:x\ge5\right)\)
\(=\dfrac{\sqrt{27}.\sqrt{\left(x-5\right)^2}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3}.\sqrt{3^2}.\left|x-5\right|}{\sqrt{3}}\)
\(=3\left(x-5\right)\)
\(=3x-15\)
\(2,\dfrac{\sqrt{\left(x-4\right)^2}}{\sqrt{9\left(x-4\right)^2}}\left(dkxd:x< 4\right)\)
\(=\dfrac{\left|x-4\right|}{\sqrt{9}.\left|x-4\right|}\)
\(=\dfrac{1}{\sqrt{3}^2}\)
\(=\dfrac{1}{3}\)
\(1,\dfrac{\sqrt{27\left(x-5\right)^2}}{\sqrt{3}}\\ =\dfrac{\sqrt{27}.\sqrt{\left(x-5\right)^2}}{\sqrt{3}}\\ =\dfrac{3\sqrt{3}.\left|x-5\right|}{\sqrt{3}}=3.\left(x-5\right)=3-15\\ 2,\dfrac{\sqrt{\left(x-4\right)^2}}{\sqrt{9\left(x-4\right)^2}}\\ =\dfrac{\left|x-4\right|}{\sqrt{9}.\sqrt{\left(x-4\right)^2}}\\ =\dfrac{\left|x-4\right|}{\sqrt{9}.\left|x-4\right|}=\dfrac{4-x}{3.\left(4-x\right)}=\dfrac{1}{3}\)