
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với \(x\ge0;x\ne\pm16\)
\(B=\left(\frac{\sqrt{x}}{\sqrt{x}+4}+\frac{4}{\sqrt{x}-4}\right):\frac{x+16}{\sqrt{x}+2}\)
\(=\left(\frac{x-4\sqrt{x}+4\sqrt{x}+16}{x-16}\right):\frac{x+16}{\sqrt{x}-2}=\frac{\sqrt{x}-2}{x-16}\)

\(\left(\sqrt{75}+\sqrt{243}-\sqrt{48}\right):\sqrt{3}\)
\(=\sqrt{75}:\sqrt{3}+\sqrt{243}:\sqrt{3}-\sqrt{48}:\sqrt{3}\)
\(=\sqrt{75:3}+\sqrt{243:3}-\sqrt{48:3}\)
\(=\sqrt{25}+\sqrt{81}-\sqrt{16}\)
\(=5+9-4=10\)


Đặt \(A=\sqrt{\sqrt2+2\sqrt{\sqrt2-1}}+\sqrt{\sqrt2-2\sqrt{\sqrt2+1}}\).
\(A=\sqrt{\sqrt2 +2\sqrt{\sqrt2-1}}+\sqrt{\sqrt2 -2\sqrt{\sqrt2+1}}\\=> A^2=\sqrt2+2\sqrt{\sqrt2-1}+\sqrt2-2\sqrt{\sqrt2+1}\\=2\sqrt2+2\sqrt{(\sqrt2+1)(\sqrt2-1)}\\=2\sqrt2+2\\=>A=\sqrt{2\sqrt2+2}\)

\(\sqrt{0,81.a^{10}\left(x^2-2x+1\right)}=\sqrt{\left(0,9\right)^2.\left(a^5\right)^2\left(x-1\right)^2}\)
\(=0,9.\left|a^5\left(x-1\right)\right|=0,9.\left|a^5x-a^5\right|\)

=\(\left(\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\sqrt{x}+3}\right).\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
=\(\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)+\sqrt{x}\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(x-9\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
=\(\dfrac{2x+6\sqrt{x}+\sqrt{x}\left(x-\sqrt{x}-6\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}.\dfrac{1}{\sqrt{x}}\)
=\(\dfrac{2x+6\sqrt{x}+x\sqrt{x}-x-6\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+x\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)

Ta có: \(\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14+18-6\sqrt{28}+6\sqrt{28}\)
=32

\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}+\dfrac{1}{2-\sqrt{x}}\left(đk:x\ge0;x\ne4\right)\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-2}\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{3+2\sqrt{x}-4-\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{1}{\sqrt{x}+1}\)
\(S=\left(\dfrac{1}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\left(đk:x\ge0;x\ne1\right)\)
\(S=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\)
\(S=\dfrac{\sqrt{x}-2+x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{x+4\sqrt{x}+4}{1-\sqrt{x}}\)
\(S=\dfrac{x+3\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(S=\dfrac{\left(x+3\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\left(1-\sqrt{x}\right)}\)
(đến đoạn này thì trong ngoặc ko tách ra đc nữa nên mik nghĩ là đến đây là xong, nếu sai thì bn nói mik)
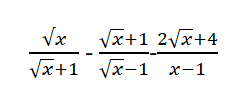
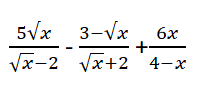

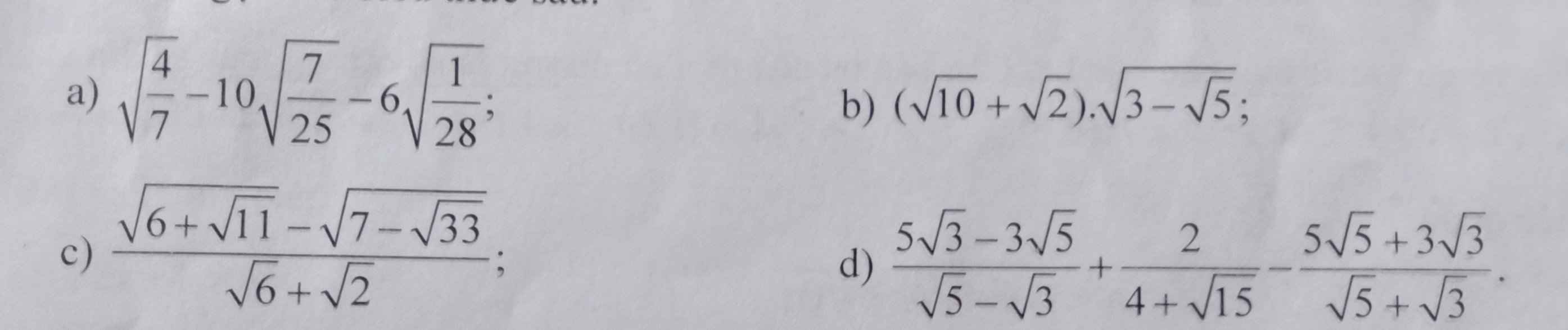 rút gọn giúp mình vs ạ
rút gọn giúp mình vs ạ 
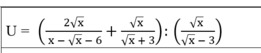
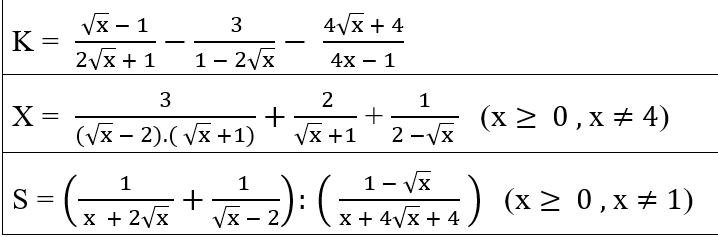
a: \(=\dfrac{x-\sqrt{x}-x-2\sqrt{x}-1-2\sqrt{x}-4}{x-1}\)
\(=\dfrac{-5\sqrt{x}-5}{x-1}=\dfrac{-5}{\sqrt{x}-1}\)
b: \(=\dfrac{5x+10\sqrt{x}+\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)-6x}{x-4}\)
\(=\dfrac{-x+10\sqrt{x}+x-5\sqrt{x}+6}{x-4}\)
\(=\dfrac{5\sqrt{x}+6}{x-4}\)