
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn ơi !!
20000 + 15000 + 9000 + 6000 = 50000 ( đồng ) mà...

\(\dfrac{32.9.11}{12.24.22}\) = \(\dfrac{8.4.3.3.11}{3.4.8.3.11.2}\) = \(\dfrac{1}{2}\)
\(\dfrac{32.9.11}{12.24.22}=\dfrac{8.4.3.3.11}{3.4.8.3.11.2}=\dfrac{1}{2}\)

\(\dfrac{72\times75}{125\times108}\) = \(\dfrac{36\times2\times25\times3}{25\times5\times36\times3}\) = \(\dfrac{2}{5}\)

Bước rút gọn 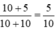 là sai vì không có tính chất
là sai vì không có tính chất 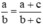 .
.
Sửa lại như sau: 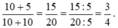

\(\dfrac{3001500}{1010012}=\dfrac{3001500:116}{1010012:116}=\dfrac{25875}{8707}\)

A = 5 + 5 ^ 2 + 5 ^ 3 + ... + 5 ^ 50
5 A = 5 ^ 2 + 5 ^ 3 + 5 ^ 4 + ... + 5 ^ 51
5 A - A = ( 5 ^ 2 + 5 ^ 3 + 5 ^ 4 + ... + 5 ^ 51 )
- ( 5 + 5 ^ 2 + 5 ^ 3 + ... + 5 ^ 50 )
4 A = 5 ^ 51 - 5
A = \(\frac{5^{51}-5}{4}\)
A=5^1+5^21+5^3+...+5^50
5^1A=5(5^1+5^2+5^3+..+5^50)
5A=5^2+5^3+..+5^50+5^51
5A-A=(5^2+5^3+..+5^50+5^51)-(5^1+5^2+5^3+..+5^50)
4A=5^51-5^1
A=(5^51-5^1):4

Ta tìm UCLN của tử số và mẫu số sau đó Lấy cả tử lẫn mẫu chia cho UCLN đó là ra 1 phân số tối giản. Tick tui đi
\(\frac{9^{14}.25^5.8^2.8^7}{18^{12}.625^3.24^3}=\frac{3^{28}.5^{10}.8^9}{2^{12}.9^{12}.5^{12}.3^3.2^9}\)\(=\frac{3^{28}.5^{10}.2^{27}}{2^{21}.5^{12}.3^{24}.3^3}=\frac{3^{28}.5^{10}.2^{27}}{2^{21}.5^{12}.3^{27}}\) \(=\frac{3.2^6}{5^2}=\frac{192}{25}=7,68\)
thanks