Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(y=\dfrac{cotx}{cosx-1}\)
Đk:\(cosx-1\ne0\Leftrightarrow cosx\ne1\)\(\Leftrightarrow x\ne k\pi,k\in Z\)
\(D=R\backslash\left\{k\pi;k\in Z\right\}\)
Ý C
a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
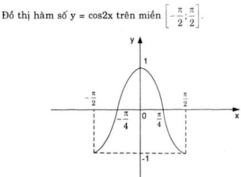
Từ đó suy ra
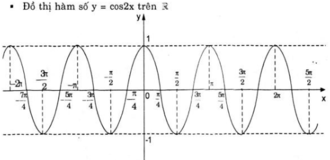
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
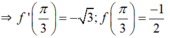
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
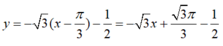
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
⇒ 
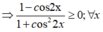
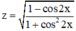luôn xác định với mọi x ∈ R.
sin8x + 5 ≥ 0 sin8x ≥ -5
Vì giá trị của sin(x) nằm trong khoảng [-1, 1], nên ta có: -1 ≤ sin8x ≤ 1 -1 - 5 ≤ sin8x + 5 ≤ 1 + 5 -6 ≤ sin8x + 5 ≤ 6
Vậy, miền xác định của hàm số là D = R (tất cả các số thực).
Đáp án: A. D = R.
Để tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = √(sin3x), ta cần xem xét giá trị của hàm số trong miền xác định.Vì giá trị của hàm số sin(x) nằm trong khoảng [-1, 1], nên giá trị của hàm số sin3x nằm trong khoảng [-1, 1]. Vì căn bậc hai của một số không âm không thể nhỏ hơn 0, nên giá trị của hàm số y = √(sin3x) nằm trong khoảng [0, 1].
Vậy, giá trị lớn nhất của hàm số là M = 1 và giá trị nhỏ nhất là m = 0.
Đáp án: D. M = 1; m = 0.
a) Ta có sin4(x + kπ/2) = sin(4x + k2π) = sin4x với k ∈ Z.
Từ đó suy ra hàm số y = sin4x là hàm số tuần hoàn với chu kì π/2.
Vì hàm số y = sin4x là hàm số lẻ nên đồ thị của nó có tâm đối xứng là gốc tọa độ O.
Các hàm số y = sin4x (C1) và y = sin4x + 1 (C2) có đồ thị như trên hình 1 và hình 2.
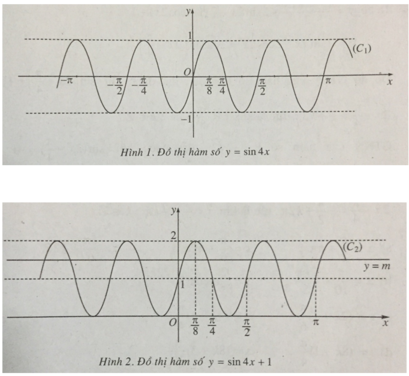
b) Vì sin4x + 1 = m ⇔ sin4x = m – 1
và -1 ≤ sin4x ≤ 1
nên -1 ≤ m – 1 ≤ 1
⇔ 0 ≤ m ≤ 2.
Từ đó, phương trình (1) có nghiệm khi 0 ≤ m ≤ 2 và vô nghiệm khi m > 2 hoặc m < 0.
c) Phương trình tiếp tuyến của (C2) có dạng
y - y o = y ’ ( x o ) ( x - x o ) .
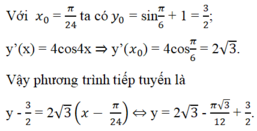
Hàm số xác định khi: \(\sin x - 1\; \ne 0\; \Leftrightarrow \sin x \ne 1\; \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi ,\;\;k \in \mathbb{Z}\)
Vậy ta chọn đáp án B
Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C
Đáp án D
Hàm số có tập xác định R khi m cosx + 1 > 0, ∀x (*) .
Khi m = 0 thì (*) luôn đúng nên nhận giá trị m = 0.
Khi m > 0 thì mcosx + 1 ∈ [-m + 1; m + 1] nên (*) đúng khi -m + 1 > 0 => 0 < m < 1.
Khi m < 0 thì mcosx + 1 ∈ [m + 1; -m + 1] nên (*) đúng khi m + 1 > 0 => -1 < m < 0
Vậy giá trị m thoả mãn là -1 < m < 1.
ĐKXĐ: \(sin^2x-cos^2x\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
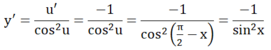
Chọn C