K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 1 2018
mk kb nha mk lp 7 nè
hi
mk là fan boboiboy nha
và ai chơi nr sv1 thì kb với mk nhé ko chơi cũng kb
XO
26 tháng 10 2019
a)(x - 1) x + 2 = (x - 1)x + 4
=> (x - 1) x + 4 - (x - 1)x + 2 = 0
=> (x - 1)x + 2 . [(x - 1)2 - 1] = 0
=> \(\orbr{\begin{cases}\left(x-1\right)^{x+2}=0\\\left(x-1\right)^2-1=0\end{cases}\Rightarrow\orbr{\begin{cases}\left(x-1\right)^{x+2}=0^{x+2}\\\left(x-1\right)^2=1^2\end{cases}\Rightarrow}\orbr{\begin{cases}x-1=0\\x-1=\pm1\end{cases}}}\)
Nếu x - 1 = 0
=> x = 1
Nếu x - 1 = - 1
=> x = 0
Nếu x - 1 = 1
=> x = 2
Vậy \(x\in\left\{0;1;2\right\}\)
b) \(\left(1,78^{2x-2}-1,78^x\right):1,78^x=0\)
\(\Rightarrow1,78^{2x-2}:1,78^x-1,78^x:1,78^x=0\)
\(\Rightarrow1,78^{x-2}-1=0\)
\(\Rightarrow1,78^{x-2}=1\)
\(\Rightarrow1,78^{x-2}=1,78^0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
Vậy x = 2
HG
2
17 tháng 7 2021
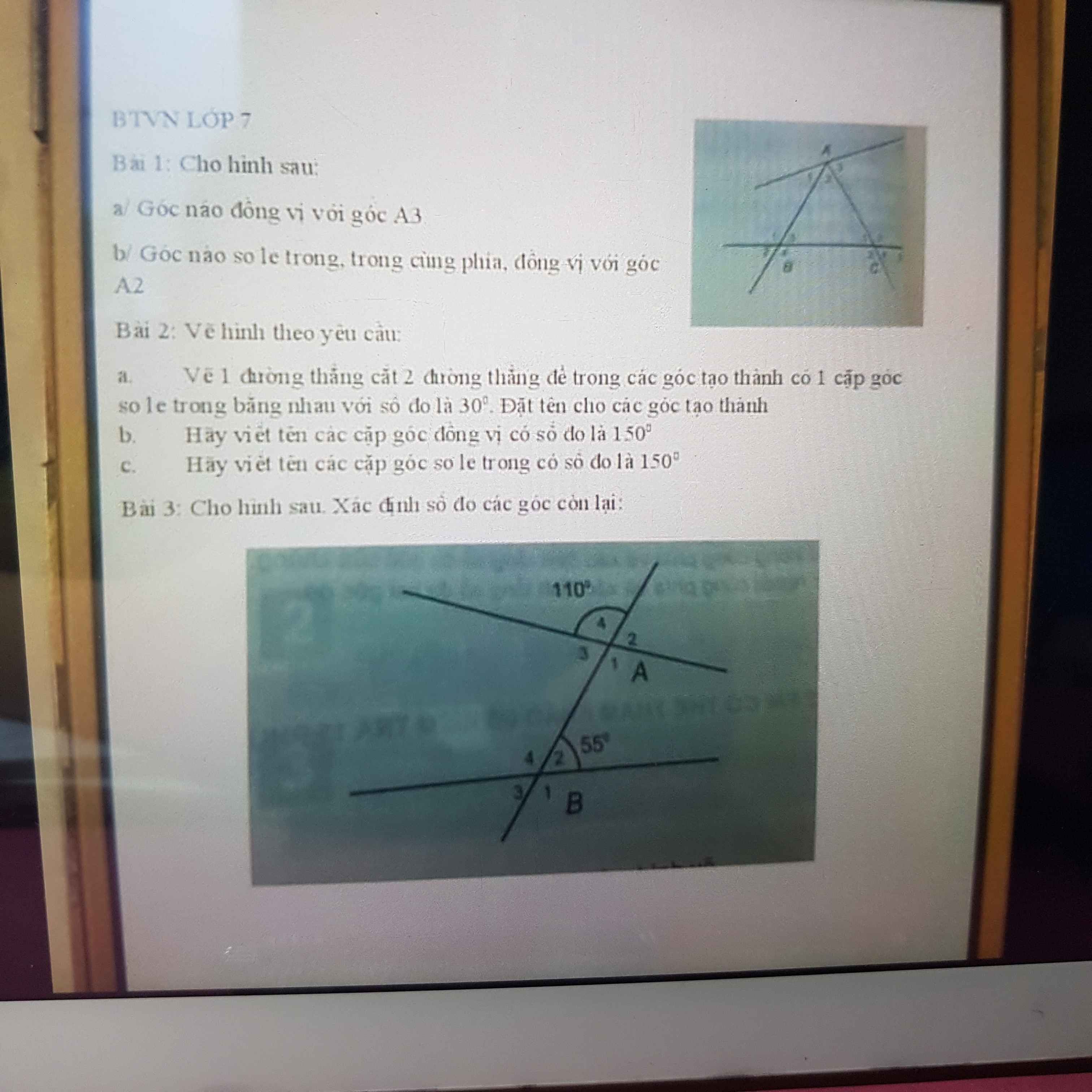
Bài 3:
\(\widehat{A_1}=110^0;\widehat{A_2}=70^0;\widehat{A_3}=70^0\)
\(\widehat{B_3}=55^0;\widehat{B_4}=125^0;\widehat{B_1}=125^0\)
B
2
27 tháng 1 2022
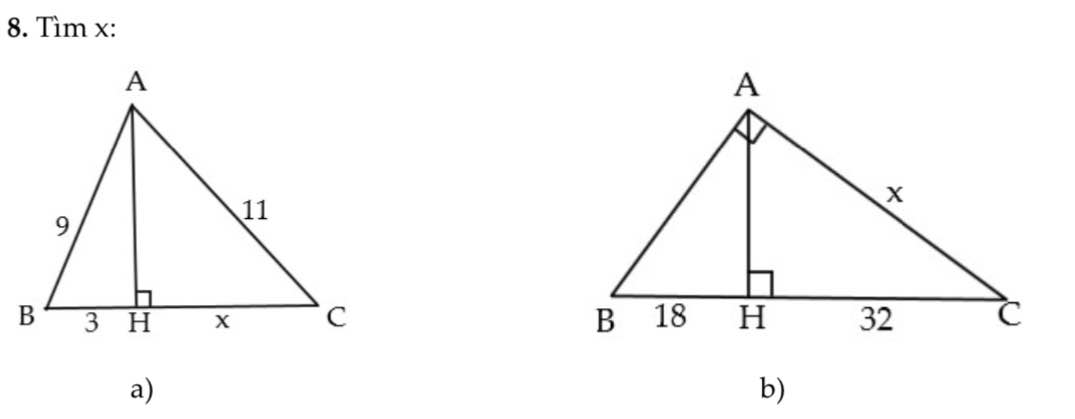
a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)
16 tháng 5 2022
a: \(A=M-N+P\)
\(=-2x^2+xy^2+3x-3x^3+2xy^2-4x+5x^3-3xy^2-x^2+2x-1\)
\(=\left(-2x^2-x^2\right)+\left(5x^3-3x^3\right)+\left(xy^2+2xy^2-3xy^2\right)+\left(3x-4x+2x\right)-1\)
\(=+2x^3-3x^2+x-1\)
b: Bạn xem lại đề, biểu thức này không có giá trị lớn nhất
uk típ