Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số \(y = 4x + 2\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = 4;b = 2\).
b) Hàm số \(y = 5 - 3x = - 3x + 5\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = - 3;b = 5\).
c) Hàm số \(y = 2 + {x^2}\) không phải là hàm số bậc nhất vì không có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\).
d) Hàm số \(y = - 0,2x\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = - 0,2;b = 0\).
e) Hàm số \(y = \sqrt 5 x - 1\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = \sqrt 5 ;b = - 1\).
a) \(y=4x+2\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)
b) \(y=5-3x\Rightarrow\left\{{}\begin{matrix}a=-2\\b=5\end{matrix}\right.\)
c) \(y=2+x^2\) không phải hàm số bậc nhất.
d) \(y=0,2x\Rightarrow\left\{{}\begin{matrix}a=-0,2\\b=0\end{matrix}\right.\)
e) \(y=\sqrt[]{5}x-1\Rightarrow\left\{{}\begin{matrix}a=\sqrt[]{5}\\b=-1\end{matrix}\right.\)

Câu 1: B
Câu 2: D
Bài 1: Các hàm số bậc nhất là
a: y=3x-2
a=3; b=-2
d: y=-2(x+5)
=-2x-10
a=-2; b=-10
e: \(y=1+\dfrac{x}{2}\)
\(a=\dfrac{1}{2};b=1\)
bạn ơi câu e minh viết là 1+x phần 2 bạn xem lai nha
câud mình viết thiếu là y = -2. (x+5) -4

Đáp án đúng là D
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = - \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - 3x + 2\) là đường thẳng có hệ số góc là \(a = - 3\).
Vì cả ba đường thẳng đều có hệ số góc khác nhau nên chúng cắt nhau.
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
- Đồ thị hàm số \(y = - 3x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
Do đó điểm \(A\left( {0;2} \right)\) là giao điểm của ba đồ thị hàm số.
Vậy đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.

Các hàm số là hàm số bậc nhất:
a) y = 3x - 2
b) y = -2x
d) y = 3(x - 1)

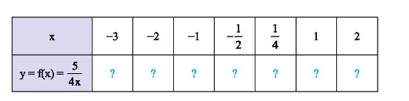
a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | \( - \dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 1 | 2 |
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) | \(\dfrac{{ - 5}}{{12}}\) | \(\dfrac{{ - 5}}{8}\) | \(\dfrac{{ - 5}}{4}\) | \(\dfrac{{ - 5}}{2}\) | 5 | \(\dfrac{5}{4}\) | \(\dfrac{5}{8}\) |

Đồ thị hai hàm số \(y = 2mx - 2\) và \(y = 6x + 3\) song song với nhau khi:
\(\left\{ \begin{array}{l}2m = 6\\ - 2 \ne 3\end{array} \right. \Rightarrow 2m = 6 \Leftrightarrow m = 6:2 \Leftrightarrow m = 3\)
Vậy \(m = 3\) thì đồ thị hai hàm số \(y = 2mx - 2\) và \(y = 6x + 3\) song song với nhau.
Để hai hàm số song song:
=> 2m=6 <=> m=3

Đồ thị hai hàm số \(y = kx - 1\) và \(y = 4x + 1\) cắt nhau khi: \(k \ne 4\).
Vậy để đồ thị hai hàm số \(y = kx - 1\) và \(y = 4x + 1\) cắt nhau thì \(k \ne 4\).

Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)

Chu vi lúc đầu là : \(\left(2+3\right)x2\left(m\right)\)
Chu vi lúc sau là : \(\left(2+x+3+x\right).2=\left(5+2x\right).2=4x+10\)
\(\Rightarrow\) Hàm số chu vi là : \(y=4x+10\) là hàm bậc nhất có :
\(\left\{{}\begin{matrix}a=4\\b=10\end{matrix}\right.\)
- Hàm số\(y = 4x - 7\) là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 4;b = - 7\).
- Hàm số \(y = {x^2}\) không là hàm số bậc nhất vì hàm số không có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
- Hàm số \(y = - 6x - 4\)là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = - 6;b = - 4\).
- Hàm số \(y = 4x\)là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 4;b = 0\).
- Hàm số \(y = \dfrac{3}{x}\) không là hàm số bậc nhất vì hàm số không có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
- Hàm số \(s = 5v + 8\) là hàm số bậc nhất vì hàm số có dạng \(s = av + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 5;b = 8\).
- Hàm số \(m = 30n - 25\) là hàm số bậc nhất vì hàm số có dạng \(m = an + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 30;b = - 25\).