Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lưu ý khi sử dung biểu thức \(s = \alpha .R\) là góc α có đơn vị là radian.
Với \({\alpha ^0} = \alpha (rad).\frac{{{{180}^0}}}{\pi }\)

Chọn đáp án C
Ta có: v 0 = 57,6 km/h = 16m/s
S = 800m; t = 40s; R = 1200m
![]()
![]()
 m/
s
2
m/
s
2
Tốc độ dài cuối cung đường: v = v 0 + a t t = 16 + 0,2.40 = 24 m/s
Gia tốc pháp tuyến cuối cùng đường:
![]() =0,48 m/s
=0,48 m/s
Gia tốc toàn phần cuối cung đường: ![]() =0,52m/
s
2
=0,52m/
s
2

Theo công thức tính chu vi đường tròn có bán kính R, ta có chiều dài của nửa đường tròn bằng πR.
Vì cung tròn của đường tròn có chiều dài là R tương ứng với góc 1 rad nên chiều dài tương ứng với góc π rad.

Theo công thức tính chu vi đường tròn có bán kính R, ta có chiều dài của nửa đường tròn bằng πR.
Vì cung tròn của đường tròn có chiều dài là R tương ứng với góc 1 rad nên chiều dài tương ứng với góc π rad.

Gia tốc hướng tâm:
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{30^2}{50}=18\)m/s2

Chọn C.
Đổi 57,6 km/h = 16 m/s
Gia tốc tiếp tuyến ở cuối cung đường:
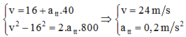
Gia tốc pháp tuyến ở cuối cung đường:
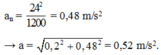
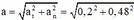
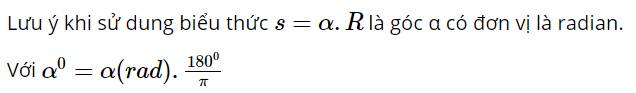
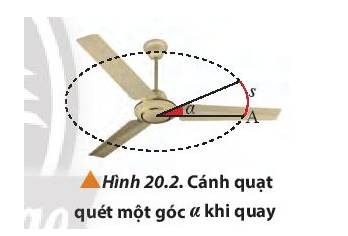

Đổi \({200^0} = \frac{{200.\pi }}{{180}} = \frac{{10\pi }}{9}(radian)\)
=> Chiều dài của cung tròn là: \(s = \alpha .R = {200^0} = \frac{{10\pi }}{9}.1,2 \approx 4,2(m)\)