Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\\ A_{min}=\dfrac{1}{9}\Leftrightarrow x=\dfrac{3}{5}\\ B=\dfrac{2009}{2008}-\left|x-\dfrac{3}{5}\right|\le\dfrac{2009}{2008}\\ B_{max}=\dfrac{2009}{2008}\Leftrightarrow x=\dfrac{3}{5}\\ C=-2\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\le1\dfrac{2}{3}\\ C_{max}=1\dfrac{2}{3}\Leftrightarrow\dfrac{1}{3}x=-4\Leftrightarrow x=-12\)

\(C=-2\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\)
\(\Rightarrow C=-2\left|\dfrac{1}{3}x+4\right|+\dfrac{5}{3}\)
mà \(-2\left|\dfrac{1}{3}x+4\right|\le0,\forall x\)
\(\Rightarrow C=-2\left|\dfrac{1}{3}x+4\right|+\dfrac{5}{3}\le\dfrac{5}{3}\)
\(\Rightarrow GTLN\left(C\right)=\dfrac{5}{3}\left(tạix=-12\right)\)

a: \(A=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

\(A=0,6+\left|\dfrac{1}{2}-x\right|\\ Vì:\left|\dfrac{1}{2}-x\right|\ge\forall0x\in R\\ Nên:A=0,6+\left|\dfrac{1}{2}-x\right|\ge0,6\forall x\in R\\ Vậy:min_A=0,6\Leftrightarrow\left(\dfrac{1}{2}-x\right)=0\Leftrightarrow x=\dfrac{1}{2}\)
\(B=\dfrac{2}{3}-\left|2x+\dfrac{2}{3}\right|\\ Vì:\left|2x+\dfrac{2}{3}\right|\ge0\forall x\in R\\ Nên:B=\dfrac{2}{3}-\left|2x+\dfrac{2}{3}\right|\le\dfrac{2}{3}\forall x\in R\\ Vậy:max_B=\dfrac{2}{3}\Leftrightarrow\left|2x+\dfrac{2}{3}\right|=0\Leftrightarrow x=-\dfrac{1}{3}\)

a, \(A=\left|x-2017\right|+\left|2018-x\right|\ge\left|x-2017+2018-x\right|=1\)
Vậy \(Min=1\Leftrightarrow2017\le x\le2018\)
b, \(B=\dfrac{x^2+4+8}{x^2+4}=1+\dfrac{8}{x^2+4}\)
Thấy : \(x^2+4\ge4\)
\(\Rightarrow B=1+\dfrac{8}{x^2+4}\le3\)
Vậy \(Max=3\Leftrightarrow x=0\)
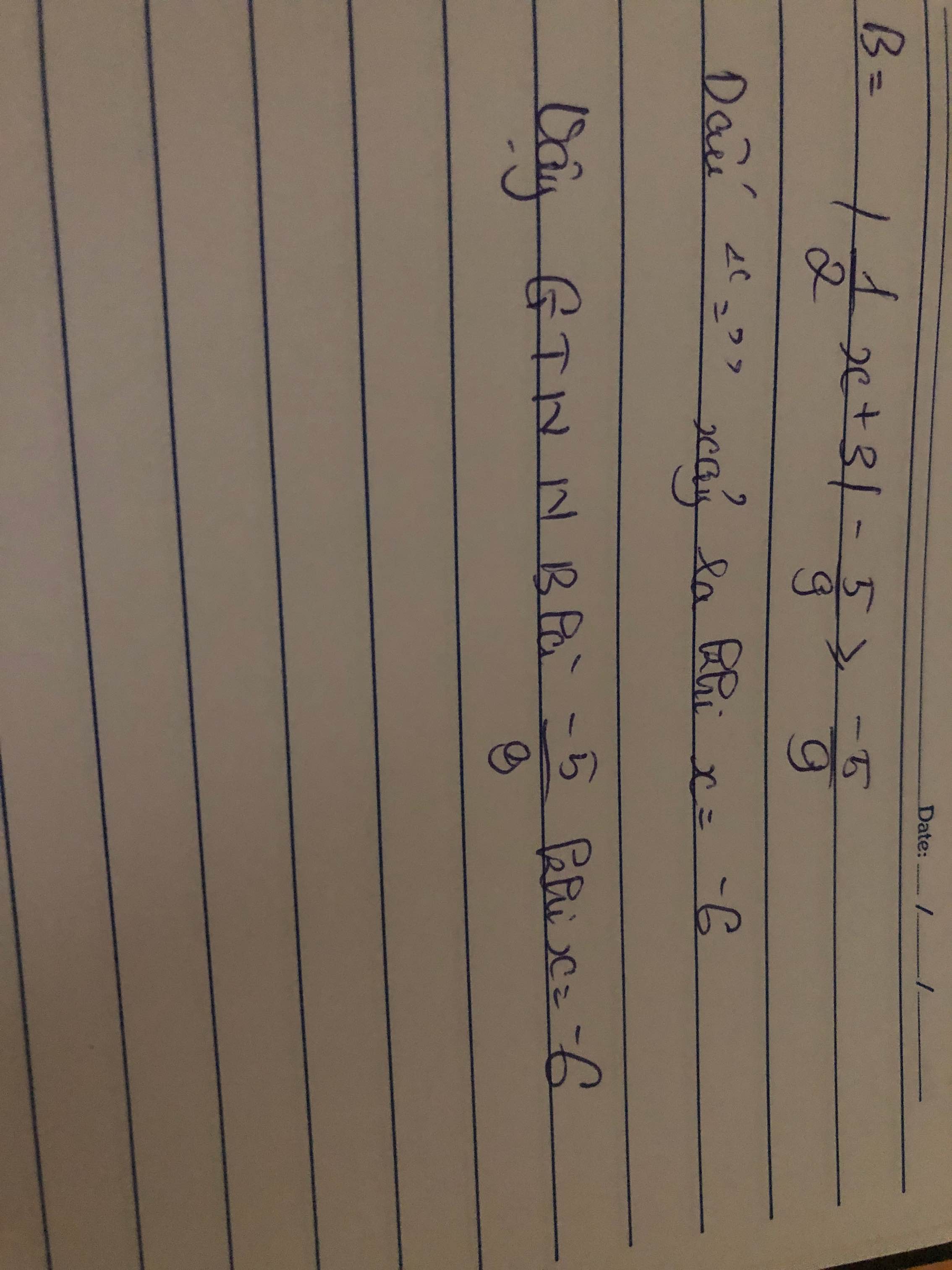
a)Vì |x-1/2|≥0
|x-1/2|-3≥0-3
A=|x-1/2|-3≥-3
=>A≥-3
Dấu ''='' xảy ra khi
x-1/2=0
x=0+1/2
x=1/2
Vậy GTNN của biểu thức đã cho là -3 khi x=1/2
b)
Vì |x-4|≥0
-|x-4|≤0
=>2/3-|x-4|≤2/3-0
2/3-|x-4|≤2/3
=>B=2/3-|x-4|≤2/3
B≤2/3
Dấu ''='' xảy ra khi
x-4=0
x=0+4
x=4
Vậy GTLN của biểu thức là 2/3 khi x=4