Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của (P) và Ox: x 2 - 4 x + m = 0 1
Để (P) cắt Ox tại hai điểm phân biệt thì (1) có hai nghiệm phân biệt x 1 , x 2
⇔ Δ ' > 0 a ≠ 0 ⇔ 4 − m > 0 1 ≠ 0 ⇔ m < 4
Giả sử A x 1 ; 0 , B x 2 ; 0 và x 1 + x 2 = 4 , x 1 x 2 = m
Ta có: O A = O B ⇔ x 1 = 3 x 2 ⇔ x 1 = 3 x 2 x 1 = − 3 x 2
Trường hợp 1: x 1 = 3 x 2 ⇒ x 1 = 3 x 2 = 1 ⇒ m = 3 (thỏa mãn)
Trường hợp 2: x 1 = - 3 x 2 ⇒ x 1 = 6 x 2 = − 2 ⇒ m = − 12 (thỏa mãn)
Vậy S = −12 + 3 = −9.
Đáp án cần chọn là: D

Phương trình hoành độ giao điểm: \(x^2-4x+m=0\) (1)
(P) cắt Ox tại 2 điểm pb \(\Leftrightarrow\left(1\right)\) có 2 nghiệm pb
\(\Leftrightarrow\Delta'=4-m>0\Rightarrow m< 4\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow x_1;x_2\) lần lượt là hoành độ OA, OB
\(\Rightarrow\left\{{}\begin{matrix}OA=\left|x_1\right|\\OB=\left|x_2\right|\end{matrix}\right.\) \(\Rightarrow\left|x_1\right|=3\left|x_2\right|\Rightarrow\left\{{}\begin{matrix}x_1=3x_2\\x_1=-3x_2\end{matrix}\right.\)
Th1: \(x_1=3x_2\) kết hợp Viet ta được: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1=3x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=3\\x_2=1\end{matrix}\right.\) \(\Rightarrow m=x_1x_2=3\)
TH2: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1=-3x_2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=6\\x_2=-2\end{matrix}\right.\)
\(\Rightarrow m=x_1x_2=-12\)
Vậy \(\left[{}\begin{matrix}m=3\\m=-12\end{matrix}\right.\)

Xét phương trình hoành độ giao điểm: x2 – 2x + m – 1 = 0
Để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương thì phương trình có hai nghiệm dương hay 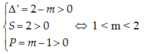
Chọn A.

Phương trình hoành độ giao điểm là:
\(x^2-4x+m=0\)
\(\text{Δ}=\left(-4\right)^2-4m=16-4m\)
Để (P) cắt Ox tại hai điểm phân biệt thì Δ>0
=>-4m+16>0
=>-4m>-16
=>m<4
(P) cắt trục Ox tại hai điểm A,B phân biệt nên \(A\left(x_A;0\right);B\left(x_B;0\right)\)
OA=3OB
=>\(OA^2=9OB^2\)
=>\(\left(x_A-0\right)^2+\left(y_A-0\right)^2=9\left[\left(x_B-0\right)^2+\left(y_B-0\right)^2\right]\)
=>\(\left(x_A\right)^2+\left(y_A\right)^2=9x_B^2+9y_B^2\)
=>\(x_A^2-9x_B^2=y_A^2-9y_B^2\)
=>\(x_A^2-9x_B^2=0\)
=>\(\left[{}\begin{matrix}x_A=3x_B\\x_A=-3x_B\end{matrix}\right.\)
Theo Vi-et, ta có:
\(x_A+x_B=4\) và \(x_A\cdot x_B=m\)
TH1: \(x_A=3x_B\)
\(x_A+x_B=4\)
=>\(3x_B+x_B=4\)
=>\(x_B=1\)
=>\(x_A=3\)
\(m=x_A\cdot x_B=1\cdot3=3\)
TH2: \(x_A=-3x_B\)
\(x_A+x_B=4\)
=>\(-3x_B+x_B=4\)
=>\(-2x_B=4\)
=>\(x_B=-2\)
\(x_A=-3\cdot x_B=-3\cdot\left(-2\right)=6\)
\(m=x_A\cdot x_B=6\cdot\left(-2\right)=-12\)