
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1, \(x^3+4x^2+4x=0\Leftrightarrow x\left(x^2+4x+4\right)=0\)
\(\Leftrightarrow x\left(x+2\right)^2=0\Leftrightarrow x=-2;x=0\)
2, \(\left(x+3\right)^2-4=0\Leftrightarrow\left(x+3-2\right)\left(x+3+2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+5\right)=0\Leftrightarrow x=-5;x=1\)
3, \(x^4-9x^2=0\Leftrightarrow x^2\left(x^2-9\right)=0\)
\(\Leftrightarrow x^2\left(x-3\right)\left(x+3\right)=0\Leftrightarrow x=0;\pm3\)
4, \(x^2-6x+9=81\Leftrightarrow\left(x-3\right)^2=9^2\)
\(\Leftrightarrow\left(x-3-9\right)\left(x-3+9\right)=0\Leftrightarrow\left(x-12\right)\left(x+6\right)=0\Leftrightarrow x=-6;x=12\)
5, em xem lại đề nhé
à lag tý @@
5, \(x^3+6x^2+9x-4x=0\Leftrightarrow x^3+6x^2+5x=0\)
\(\Leftrightarrow x\left(x^2+6x+5\right)=0\Leftrightarrow x\left(x^2+x+5x+5\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x+5\right)=0\Leftrightarrow x=-5;x=-1;x=0\)

a) x( x + 3 ) - 2x - 6 =0
=> x^2 + 3x - 2x -6 = 0
=> x^2 + x - 6 = 0
=> ( x^2 -x ) + ( 6x - 6 ) = 0
=> x( x - 1 ) + 6( x - 1 ) = 0
=> ( x - 1 )( x + 6 ) = 0
=> x = 1 hoặc x= -6
b) 9x^2 - 6x - 3 = 0
=> (9x^2 + 3x ) - ( 9x + 3 ) = 0
=> 3x(3x + 1) - 3(3x + 1 ) = 0
=> 3( 3x + 1 )(x-1)=0
=> x = -1/3 hoặc x = 1
Vũ ơi! Dòng thứ 3 xuống dòng thứ 4 câu a. Em phân tích bị sai rồi. Em có thể làm theo cách khác mà không cần phân tích ra không ? Sử dụng -2x - 6 = - 2 ( x + 3 )
Câu b. Đúng rồi.

d) \(4x^2-9-x\left(2x-3\right)=0\)
\(\Leftrightarrow4x^2-9-2x^2+3x=0\)
\(\Leftrightarrow2x^2+3x-9=0\)
\(\Delta=3^2-4.2.\left(-9\right)=9+72=81\)
Vậy pt có 2 nghiệm phân biệt
\(x_1=\frac{-3+\sqrt{81}}{4}=\frac{-3}{2}\);\(x_1=\frac{-3-\sqrt{81}}{4}=-3\)
e) \(x^3+5x^2+9x=-45\)
\(\Leftrightarrow x^3+5x^2+9x+45=0\)
\(\Leftrightarrow x^2\left(x+5\right)+9\left(x+5\right)=0\)
\(\Leftrightarrow\left(x^2+9\right)\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+9=0\\x+5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\pm3i\\x=-5\end{cases}}\)

\(x^3-9x+7x^2-63=0\)
\(\Rightarrow\left(x^3+7x^2\right)-9x-63=0\)
\(\Rightarrow x^2\left(x+7\right)-9\left(x+7\right)=0\)
\(\Rightarrow\left(x^2-9\right)\left(x+7\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x^2-9=0\\x+7=0\end{cases}\Rightarrow\orbr{\begin{cases}x^2=9\\x=-7\end{cases}\Rightarrow}\orbr{\begin{cases}x=\pm3\\x=-7\end{cases}}}\)
Vậy ...
x3−9x+7x2−63=0x3−9x+7x2−63=0
⇒(x3+7x2)−9x−63=0⇒(x3+7x2)−9x−63=0
⇒x2(x+7)−9(x+7)=0⇒x2(x+7)−9(x+7)=0
⇒(x2−9)(x+7)=0⇒(x2−9)(x+7)=0
⇒{x2−9=0x+7=0⇒{x2=9x=−7⇒{x=±3x=−7⇒{x2−9=0x+7=0⇒{x2=9x=−7⇒{x=±3x=−7
Vậy ...

9x2-6x-3=0
=>9x2-9x+3x-3=0
=>(x-1)(9x-3)=0
=>x-1=0 hoặc 9x+3 = 0
=> x=1 hoặc x=-1/3
b. x3+9x2+27x+19=0
x3+x2+8x2+8x+19x+19=0
(x+1)(x2+8x+19)=0
x+1=0 => x=-1
x2+8x+19= x2+8x+16+3=(x+4)2+3 lớn hơn hoặc bằng 3., lớn hơn 0 với moị x
a, \(\Rightarrow3\left(3x^2-2x-1\right)=0\)
\(\Rightarrow3x^2-2x-1=0\)
\(\Rightarrow x\left(3x-2\right)=1\)
\(\Rightarrow\orbr{\begin{cases}x=1\\3x-2=1\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\x=1\end{cases}}}\)
\(\Rightarrow\orbr{\begin{cases}x=-1\\3x-2=-1\end{cases}\Rightarrow}\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}\)
b,\(\Rightarrow x^3+3x^2+6x^2+9x+18x+19=0\)
\(\Rightarrow x^2\left(x+3\right)+3x\left(x+3\right)+18\left(x+3\right)-2=0\)
\(\Rightarrow\left(x+3\right)\left(x^2+3x+18\right)=2\)
Mk k co thoi gian. buoc tiep theo tu lam not nhe

\(\frac{x-1}{x^2-9x+20}+\frac{2x-2}{x^2-6x+8}+\frac{3x-3}{x^2-x-2}+\frac{4x-4}{x^2+6x+5}=0\)
\(\Leftrightarrow\frac{x-1}{\left(x-5\right)\left(x-4\right)}+\frac{2\left(x-1\right)}{\left(x-4\right)\left(x-2\right)}+\frac{3\left(x-1\right)}{\left(x-2\right)\left(x+1\right)}+\frac{4\left(x-1\right)}{\left(x+1\right)\left(x+5\right)}=0\)
\(\Leftrightarrow\left(x-1\right)\left(\frac{10}{x^2-25}\right)=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\)
PS: Điều kiện xác đinh bạn tự làm nhé

d: Ta có: \(9x^2+6x-8=0\)
\(\Leftrightarrow9x^2+12x-6x-8=0\)
\(\Leftrightarrow\left(3x+4\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
e: Ta có: \(x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
f: Ta có: \(5x\left(x-3\right)-x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)

\(a,9x^2-6x-3=0\)
\(\Leftrightarrow9x^2-6x+1-4=0\)
\(\Leftrightarrow\left(3x-1\right)^2=4\)
\(\Rightarrow3x-1=\pm2\)
\(\hept{\begin{cases}3x-1=2\Rightarrow x=1\\3x-1=-2\Rightarrow x=\frac{-1}{3}\end{cases}}\)
Vậy \(x=1\) hoặc \(x=\frac{-1}{3}\)
\(b,x^3+9x^2+27x+19=0\)
\(\Leftrightarrow x^3+9x^2+27x+27-8=0\)
\(\Leftrightarrow\left(x+3\right)^3=8\)
\(\Rightarrow x+3=2\)
\(\Rightarrow x=-1\)
Vậy \(x=-1\)
\(c,x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=3\)
\(\Leftrightarrow x\left(x^2-25\right)-\left(x^3+8\right)=3\)
\(\Leftrightarrow x^3-25x-x^3-8=3\)
\(\Leftrightarrow-25x=11\)
\(\Leftrightarrow x=\frac{-11}{25}\)
Vậy \(x=\frac{-11}{25}\)
\(9x^2-6x-3=0\)
<=> \(\left(3x\right)^2-2.3x.1+1-4=0\)
<=> \(\left(3x-1\right)^2-2^2=0\)
<=> \(\left(3x-3\right)\left(3x+1\right)=0\)
<=> \(\hept{\begin{cases}3x-3=0\\3x+1=0\end{cases}}\)
<=> \(\hept{\begin{cases}x=1\\x=\frac{-1}{3}\end{cases}}\)
\(x^3+9x^2+27x+19\) \(=0\)
<=>\(x^3+x^2+8x^2+8x+19x+19=0\)
<=> \(x^2\left(x+1\right)+8x\left(x+1\right)+19\left(x+1\right)=0\)
<=> \(\left(x^2+8x+19\right)\left(x+1\right)=0\)
mà \(x^2+8x+19>0\)
=> \(x+1=0\)
<=> \(x=-1\)
\(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=3\)
<=> \(x\left(x^2-25\right)-\left(x+2\right)\left(x-2\right)^2=3\)
<=> \(x^3-25x-\left(x^2-4\right)\left(x-2\right)=3\)
<=> \(x^3-25x-\left(x^3-2x^2-4x+8\right)=3\)
<=> \(x^3-25x-x^3+2x^2+4x-8=3\)
<=> \(2x^2-21x-8=3\)
<=> \(2x^2-21x-11=0\)
<=> \(2x^2-22x+x-11=0\)
<=> \(2x\left(x-11\right)+\left(x-11\right)=0\)
<=> \(\left(2x+1\right)\left(x-11\right)=0\)
<=> \(\hept{\begin{cases}2x+1=0\\x-11=0\end{cases}}\)
<=> \(\hept{\begin{cases}x=\frac{-1}{2}\\x=11\end{cases}}\)
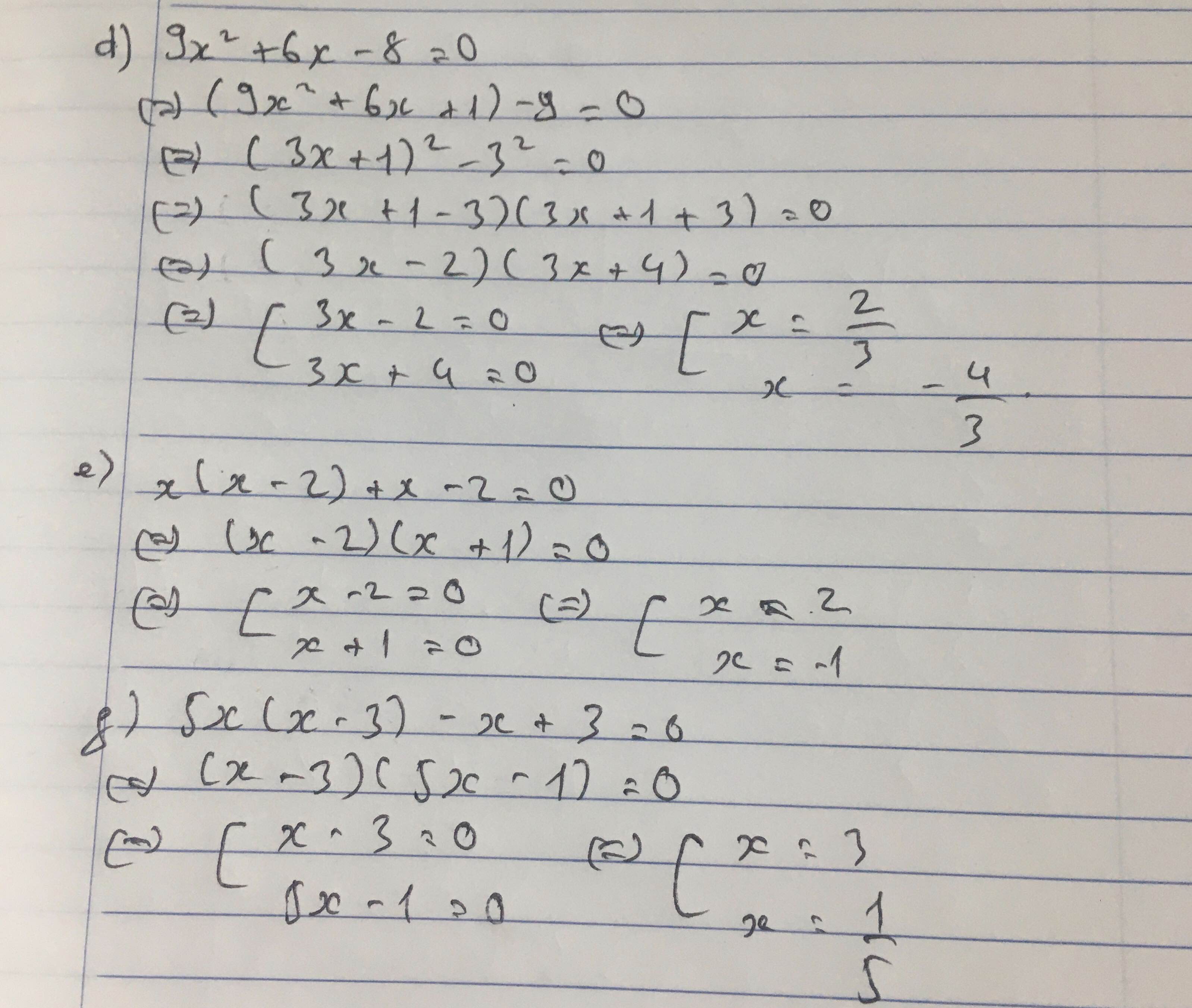 Mình trình bày trong hình ^^ Bn tham khảo nhé
Mình trình bày trong hình ^^ Bn tham khảo nhé
Ta có: \(x^3+6x^2+9x=0\)
\(\Leftrightarrow x\left(x+3\right)^2=0\)
hay \(x\in\left\{0;-3\right\}\)
x3+6x2+9x=0
⇒x(x2+6x+9)=0
⇒x(x+3)2=0
⇒\(\left[{}\begin{matrix}x=0\\\left(x+3\right)^2=0\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=0\\x+3=0\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)