Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình (5 + 2 ) x 2 + (5 - 2 )x -10 =0 có hệ số
a =5 + 2 , b = 5 - 2 , c = -10
Ta có: a +b +c =5 + 2 +5 - 2 +(-10)=0
Suy ra nghiệm của phương trình là x 1 = 1 , x 2 = c/a = (-10)/(5+ 2 )

a) 1 , 5 x 2 – 1 , 6 x + 0 , 1 = 0
Có a = 1,5; b = -1,6; c = 0,1
⇒ a + b + c = 1,5 – 1,6 + 0,1 = 0
⇒ Phương trình có hai nghiệm x 1 = 1 ; x 2 = c / a = 1 / 15 .

d) ( m – 1 ) x 2 – ( 2 m + 3 ) x + m + 4 = 0
Có a = m – 1 ; b = - (2m + 3) ; c = m + 4
⇒ a + b + c = (m – 1) – (2m + 3) + m + 4 = m -1 – 2m – 3 + m + 4 = 0
⇒ Phương trình có hai nghiệm 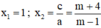

\(a=2-\sqrt{3}\) ; \(b=2\sqrt{3}\) ; \(c=-2-\sqrt{3}\)
\(\Rightarrow a+b+c=2-\sqrt{3}+2\sqrt{3}-2-\sqrt{3}=0\)
\(\Rightarrow\) Phương trình đã cho có 2 nghiệm:
\(x_1=1\) ; \(x_2=\dfrac{c}{a}=\dfrac{-2-\sqrt{3}}{2-\sqrt{3}}=-7-4\sqrt{3}\)
Dùng hệ thức Viet để tính nhẩm các nghiệm của phương trình:
a) x2 - 7x + 12 = 0; b) x2 + 7x+ 12 = 0.

a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = \(-\dfrac{-7}{1}\) = 7 = 3 + 4
x1x2 = \(\dfrac{12}{1}\) = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = \(\dfrac{-7}{1}\) = -7 = -3 + (-4)
x1x2 = \(\dfrac{12}{1}\) = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.
a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = = 7 = 3 + 4
x1x2 = = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = = -7 = -3 + (-4)
x1x2 = = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.

b. Tự đặt đk
\(x^{^2}+5\sqrt{x-3}=21\\\Leftrightarrow x^{^2}-9+5\sqrt{x-3}=12 \)
Đặt \(a=\sqrt{x-3}\) \(\left(a\ge0\right)\) Phương trình trở thành:
\(a^{^2}\left(a^{^2}+6\right)+5a=12\\ \Leftrightarrow a^{^4}+6a^{^2}+5a-12=0\\ \Leftrightarrow a^{^4}-a^{^3}+a^{^3}-a^{^2}+7a^{^2}-7a+12a-12=0\\ \Leftrightarrow\left(a-1\right)\left(a^{^3}+a^{^2}+7a+12\right)=0\\ \Leftrightarrow a=1\left(tmdk\right)\)
Ta có: vì \(a\ge0\) nên \(a^{^3}+a^{^2}+7a+12\ne0\)
Với a = 1 ta có x=4 (tmdk)

a) Phương trình 1,5x2 – 1,6x + 0,1 = 0
Có a + b + c = 1,5 – 1,6 + 0,1 = 0 nên x1 = 1; x2 = \(\dfrac{0,1}{15}\)
c) \(\left(2-\sqrt{3}\right)x^2+2\sqrt{3x}-\left(2+\sqrt{3}\right)=0\)
Có \(a+b+c=2-\sqrt{3}+2\sqrt{3}-\left(2+\sqrt{3}\right)=0\)
Nên x1 = 1, x2 = \(\dfrac{-\left(2+\sqrt{3}\right)}{2-\sqrt{3}}\) = -(2 + \(\sqrt{3}\))2 = -7 - 4\(\sqrt{3}\)
d) (m – 1)x2 – (2m + 3)x + m + 4 = 0
Có a + b + c = m – 1 – (2m + 3) + m + 4 = 0
Nên x1 = 1, x2 = \(\dfrac{m+4}{m-1}\)
a) Phương trình 1,5x2 – 1,6x + 0,1 = 0
Có a + b + c = 1,5 – 1,6 + 0,1 = 0 nên x1 = 1; x2 =
b) Phương trình √3x2 – (1 - √3)x – 1 = 0
Có a – b + c = √3 + (1 - √3) + (-1) = 0 nên x1 = -1, x2 = =
c) (2 - √3)x2 + 2√3x – (2 + √3) = 0
Có a + b + c = 2 - √3 + 2√3 – (2 + √3) = 0
Nên x1 = 1, x2 = = -(2 + √3)2 = -7 - 4√3
d) (m – 1)x2 – (2m + 3)x + m + 4 = 0
Có a + b + c = m – 1 – (2m + 3) + m + 4 = 0
Nên x1 = 1, x2 =

(x2−2x+1+2)(2x−x2−1+7)=18(x2-2x+1+2)(2x-x2-1+7)=18
⇒[(x−1)2+2][7−(x−1)2]=18(1)⇒[(x-1)2+2][7-(x-1)2]=18(1)
Đặt (x−1)2=a(x-1)2=a
(1)⇔(a+2)(7−a)=18(1)⇔(a+2)(7-a)=18
⇒−a2+5a+14=18⇒-a2+5a+14=18
⇒a2−5a+4=0⇒a2-5a+4=0
Ta có a+b+c=1−5+4=0a+b+c=1-5+4=0
⇒a1=1⇒a1=1
a2=41=4a2=41=4
Thay (x−1)2=a(x-1)2=a vào ta được
[(x−1)2=1(x−1)2=4[(x−1)2=1(x−1)2=4
⇒⎡⎢ ⎢ ⎢⎣x−1=1x−1=−1x−1=2x−1=−2⇒[x−1=1x−1=−1x−1=2x−1=−2
⇒⎡⎢ ⎢ ⎢⎣x=2x=0x=3x=−1⇒[x=2x=0x=3x=−1
Vậy nghiệm của phương trình là x={−1;0;2;3}
a) - 5 x 2 + 3 x + 2 = 0 ;
Nhận thấy phương trình có a + b + c = 0 nên phương trình có 2 nghiệm
x 1 = 1 ; x 2 = c / a = ( - 2 ) / 5
b) 2004 x 2 + 2005 x + 1 = 0
Nhận thấy phương trình có a - b + c = 0 nên phương trình có 2 nghiệm
x 1 = - 1 ; x 2 = - c / a = ( - 1 ) / 2004