
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1.
$=153^2+2.47.153+47^2=(153+47)^2=200^2=40000$
2.
$=1,24^2-2.1,24.0,24+0,24^2=(1,24-0,24)^2=1^2=1$
3. Không phù hợp để tính nhanh
4.
$=15^8-(15^8-1)=1$
5.
$=(1^2-2^2)+(3^2-4^2)+(5^2-6^2)+...+(2019^2-2020^2)$
$=(1-2)(1+2)+(3-4)(3+4)+(5-6)(5+6)+...+(2019-2020)(2019+2020)$
$=(-1)(1+2)+(-1)(3+4)+(-1)(5+6)+....+(-1)(2019+2020)$
$=(-1)(1+2+3+4+....+2019+2020)=(-1).2020(2020+1):2=-2041210$
6:
\(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =1.\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^4-1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^8-1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^{2020}-1\right)\left(2^{2020}+1\right)+1\\ =2^{4040}-1+1=2^{4040}\)

B=\(3^{24}-\left(27^4+1\right)\left(9^6+1\right)=-1062883\)A=123(123+154)+772=123.277+772=34843
C=\(85^2+75^2+65^2+55^2-45^2-35^2-25^2-15^2=16000\)

`a, 126^2 - 152 . 126 + 5776.`
`= 126^2 - 2 . 76 . 126 + 76^2`
`= (126+76)^2 = 202^2 = 40804`
`b, 3^8 . 5^8 - (15^4-1)(15^4+1)`
`= 15^8 - 15^8 + 1`
`= 1`

B = (154 - 1)(154 + 1) - 38 . 58
= 158 - 1 - (3.5)8
= 158 - 1 - 158 = -1

- Gỉa sử a là nghiệm nguyên của P(X) .
- Khi đó P(x) có dạng : \(P_{\left(x\right)}=\left(x-a\right)g\left(x\right)\)
- Theo bài ra ta có : \(P\left(x\right)=\left(2-a\right)\left(3-a\right)\left(4-a\right)g\left(2\right)g\left(3\right)g\left(4\right)=154\)
Thấy : \(\left(2-a\right)\left(3-a\right)\left(4-a\right)⋮3\forall a\in Z\)
Mà \(154⋮̸3\)
Vậy đa thức P(x) không có nghiệm nguyên .


A=123^2 + 54.123 + 77^2
= 123^2 + 2.123.77 + 77^2 - (154-54).123
= (123+77)^2 - 100.123
= 200^2 -12300
= 40000-12300
= 27700.

a) \(A=123\left(123+154\right)+77^2\)
\(A=123^2+\left(123.154\right)+77^2=\left(123+77\right)^2=200^2=400\)
b) \(B=3^{24}-\left(2^{47}+1\right)\left(9^6-1\right)\)
\(B=3^{24}-\left(3^{12}-1\right)\left(3^{12}+1\right)\)
\(B=3^{24}-3^{24}+1=1\)
c) \(C=85^2+75^2+65^2+55^2-45^2-35^2-25^2-15^2\)
\(C=\left(85^2-15^2\right)+\left(75^2-25^2\right)+\left(65^2-35^2\right)+\left(55^2-45^2\right)\)
\(C=\left(85+15\right)\left(85-15\right)+\left(75+25\right)\left(75-25\right)+\left(65+35\right)\left(65-35\right)\left(55+45\right)\left(55-45\right)\)
\(C=100\left(60+50+40+30+20+10\right)\)
\(C=100.210=21000\)
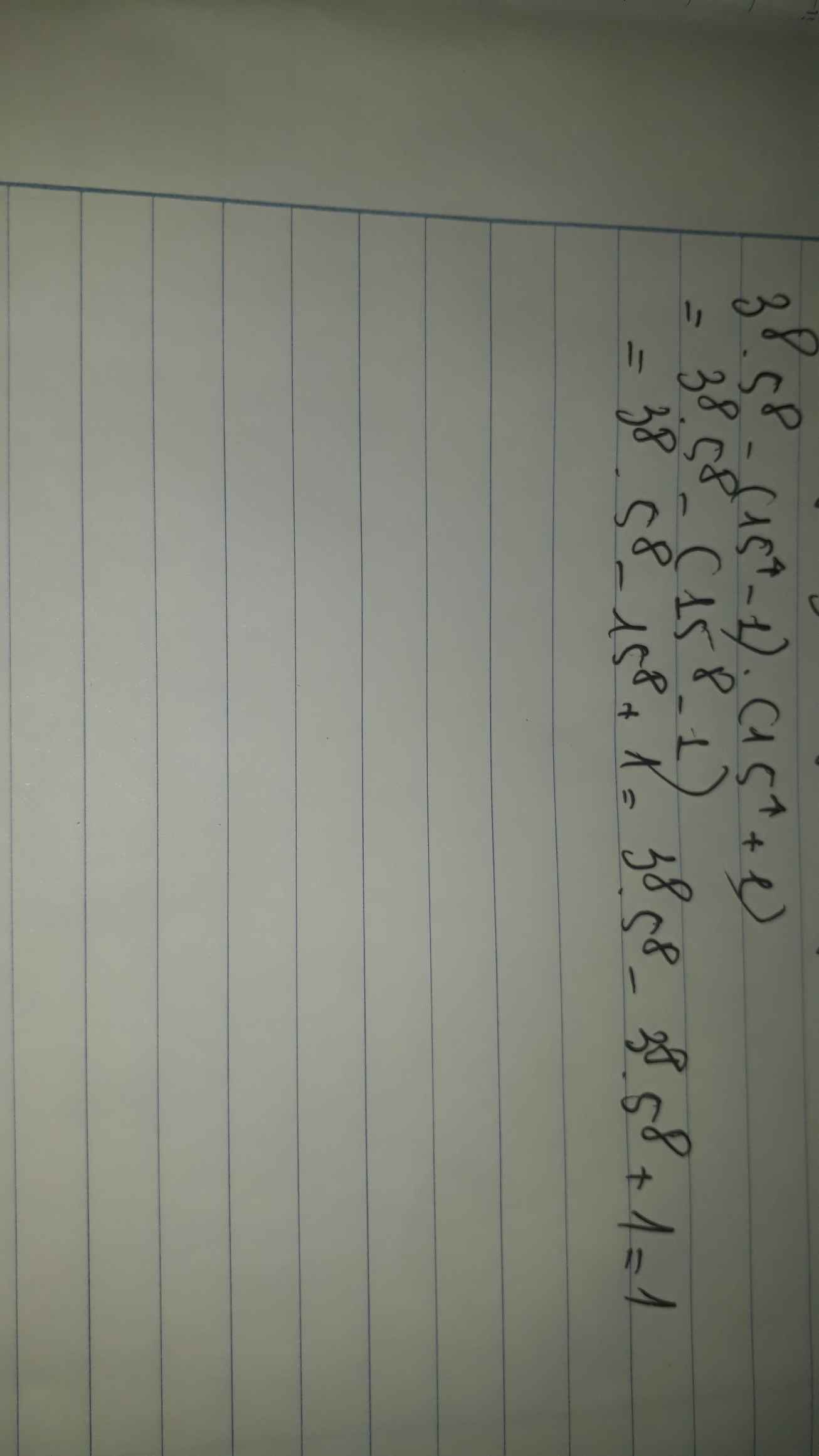
B=(154 -1).(154+1)-38.58 =158-1-(3.5)8=158-1-158 =-1
\(\left(15^4-1\right)\left(15^4+1\right)-3^8.5^8\)
= \(15^8-1-3^8.5^8\)
= \(\left(3.5\right)^8-1-3^8.5^8\)
=\(3^8.5^8-1-3^8.5^8\)
=\(-1\)