
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tính tổng các số hạng của 1 cấp số cộng có a1=100; an=1000; d=1

Áp dụng hằng đẳng thức \(\left(a+b\right)\left(a-b\right)=a^2-b^2\)ta đc:
\(\left(x+2y+z\right)\left(x+2y-z\right)=\left[\left(x+2y\right)+z\right]\left[\left(x+2y\right)-z\right]\)
\(=\left(x+2y\right)^2-z^2\)
\(=x^2+4xy+4y^2-z^{ }\)
( x + 2y + z ) ( x + 2y - z )
<=> ( x + 2y)2 - z2
<=> x2 + 4xy + 4y2 - z2
^^ Học tốt!




B2:
a) \(\dfrac{1}{x+2}+\dfrac{1}{\left(x+2\right)\left(4x+7\right)}\left(ĐK:x\ne-2;x\ne-\dfrac{7}{4}\right)\)
\(=\dfrac{4x+7}{\left(x+2\right)\left(4x+7\right)}+\dfrac{1}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4x+8}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4\left(x+2\right)}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4}{4x+7}\)
b) \(\dfrac{3x+5}{x^2-5x}-\dfrac{x-25}{25-5x}\left(ĐK:x\ne0;x\ne5\right)\)
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5x-25}\)
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5\left(x-5\right)}\)
\(=\dfrac{5\left(3x+5\right)}{5x\left(x-5\right)}+\dfrac{x\left(x-25\right)}{5x\left(x-5\right)}\)
\(=\dfrac{15x+25+x^2-25x}{5x\left(x-5\right)}\)
\(=\dfrac{x^2-10x+25}{5x\left(x-5\right)}\)
\(=\dfrac{x^2-2\cdot x\cdot5+5^2}{5x\left(x-5\right)}\)
\(=\dfrac{\left(x-5\right)^2}{5x\left(x-5\right)}\)
\(=\dfrac{x-5}{5x}\)


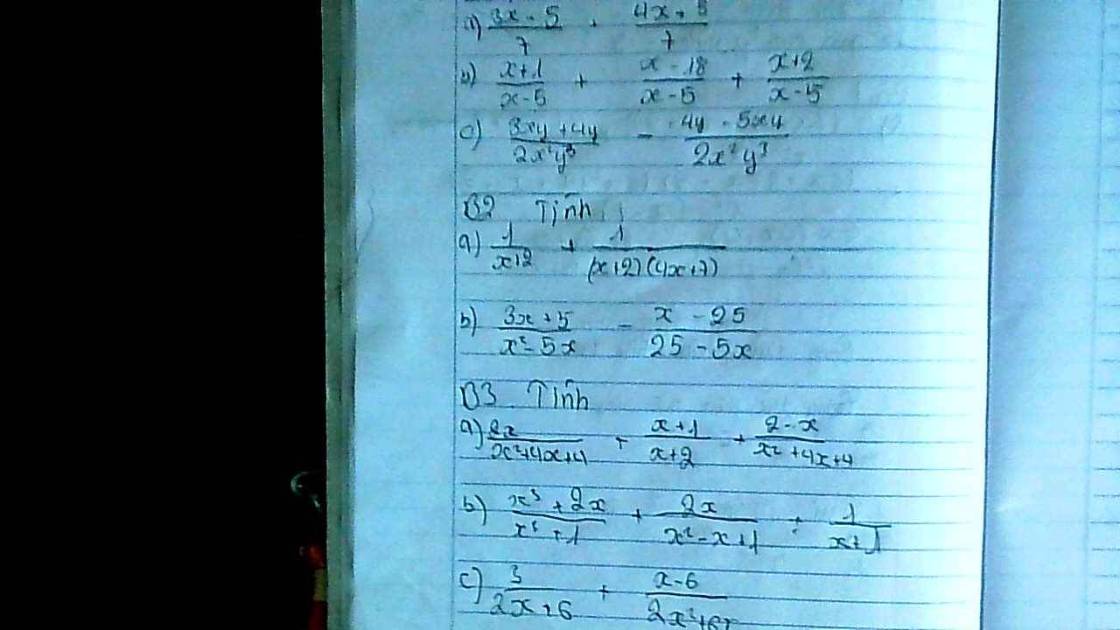
53.47 = 2491
Kết bạn nhé
\(53\cdot47=2491\)