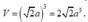Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có ![]()
![]() .
.
Do đó ![]()
![]()

Đáp án B
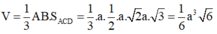
Phương án nhiễu.
A. Sai vì 2 cách: một là thấy số 1 3 cứ chọn, hai là trong công thức thể tích thiếu 1 3 diện tích đáy.
C. Sai vì thiếu 1 3 trong công thức thể tích.

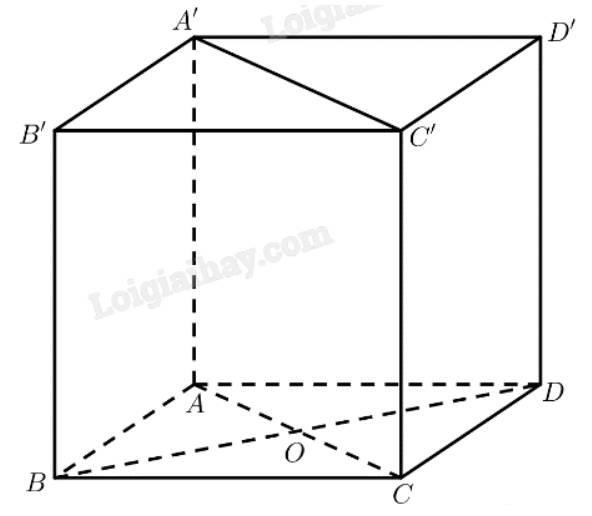
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)

a) Khi a = 1dm:
Diện tích một mặt `(S) = a^2 = 1^2 = 1dm^2`
Thể tích `(V) = a^3 = 1^3 = 1dm^3`
Khi a = 3dm:
Diện tích một mặt `(S) = a^2 = 3^2 = 9dm^2`
Thể tích `(V) = a^3 = 3^3 = 27dm^3`
b) Để S = `25dm^2`, ta cần tìm giá trị của a. Ta có:
`a^2 = 25`
=> `a = √25 = 5dm`
c) Để V = `64dm^3`, ta cần tìm giá trị của a. Ta có:
`a^3 = 64`
=> `a = ∛64 = 4dm`

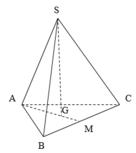
Diện tích đáy lớn là: \(S = \frac{{{{\left( {2{\rm{a}}} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Diện tích đáy bé là: \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}\left( {{a^2}\sqrt 3 + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} + \frac{{{a^2}\sqrt 3 }}{4}} \right) = \frac{{7\sqrt 2 }}{{12}}{a^3}\)
Chọn C.
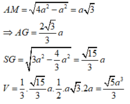
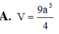
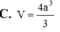


Đáp án C
Ta có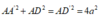
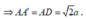
Vậy cạnh của hình lập phương trình có cạnh độ dài 2 a.
Vậy