Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên mặt phẳng tọa độ Oxy, cho điểm M(2;5). Khi đó:
A. Đường tròn (M;5) cắt hai trục Ox,Oy.
B. Đường tròn (M;5) cắt trục Ox và tiếp xúc với trục Oy.
C. Đường tròn (M;5) tiếp xúc với trục Ox và cắt trục Oy.
D. Đường tròn (M;5) không cắt cả hai trục Ox,Oy.
Học tốt!

a: Thay y=0 vào (1), ta được:
2x-1=0
hay \(x=\dfrac{1}{2}\)
Thay x=0 vào (1), ta được:
\(y=2\cdot0-1=-1\)
Vậy: \(A\left(\dfrac{1}{2};0\right)\); B(0;-1)
Thay y=0 vào (2), ta được:
x-1=0
hay x=1
Thay x=0 vào (2), ta được:
y=0-1=-1
Vậy: M(1;0); N(0;-1)

1: Thay x=0 và y=4 vào (d), ta được:
\(0\left(m^2+1\right)+m+2=4\)
=>m+2=4
=>m=2
2: tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x\left(m^2+1\right)+m+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{-m-2}{m^2+1}\\y=0\end{matrix}\right.\)
Tọa độ B là: \(\left\{{}\begin{matrix}x=0\\y=0\left(m^2+1\right)+m+2=m+2\end{matrix}\right.\)
vậy: O(0;0); \(A\left(\dfrac{-m-2}{m^2+1};0\right);B\left(0;m+2\right)\)
\(OA=\sqrt{\left(\dfrac{-m-2}{m^2+1}-0\right)^2+\left(0-0\right)^2}=\sqrt{\dfrac{\left(m+2\right)}{m^2+1}}^2=\dfrac{\left|m+2\right|}{m^2+1}\)
\(OB=\sqrt{\left(0-0\right)^2+\left(m+2-0\right)^2}=\sqrt{0^2+\left(m+2\right)^2}=\left|m+2\right|\)
Vì Ox\(\perp\)Oy nên ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{\left(m+2\right)^2}{m^2+1}\)
Để \(S_{OBA}=\dfrac{1}{2}\) thì \(\dfrac{1}{2}\cdot\dfrac{\left(m+2\right)^2}{m^2+1}=\dfrac{1}{2}\)
=>\(\dfrac{\left(m+2\right)^2}{m^2+1}=1\)
=>\(\left(m+2\right)^2=m^2+1\)
=>\(m^2+4m+4=m^2+1\)
=>4m+4=1
=>4m=-3
=>\(m=-\dfrac{3}{4}\)

1: Tọa độ A là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m+1\right)\cdot x+3=0\left(m+1\right)+3=3\end{matrix}\right.\)
Vậy: A(0;3)
2: Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\left(m+1\right)x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x\left(m+1\right)=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{3}{m+1}\end{matrix}\right.\)
=>\(B\left(\dfrac{-3}{m+1};0\right)\)
\(OB=\sqrt{\left(-\dfrac{3}{m+1}-0\right)^2+\left(0-0\right)^2}=\dfrac{3}{\left|m+1\right|}\)
\(OA=\sqrt{\left(0-0\right)^2+\left(3-0\right)^2}=3\)
OA=2OB
=>\(3=\dfrac{6}{\left|m+1\right|}\)
=>|m+1|=2
=>\(\left[{}\begin{matrix}m+1=2\\m+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)

1: Tọa độ A là:
y=0 và 4x+m-3=0
=>x=(-m+3)/4 và y=0
=>OA=|m-3|/4
Tọa độ B là:
x=0 và y=m-3
=>OB=|m-3|
Theo đề, ta có: 1/2*(m-3)^2/4=9
=>(m-3)^2/4=18
=>(m-3)^2=72
=>\(m=\pm6\sqrt{2}+3\)
2:
PTHĐGĐ là:
x^2-4x-m+3=0
Δ=(-4)^2-4*(-m+3)=16+4m-12=4m+4
Để (P) cắt (d) tại hai điểm phân biệt thì 4m+4>0
=>m>-1
(4-x1)(x2-1)=2
=>4x2-4-x1x2+1=2
=>x2(x1+x2)-3-(-m+3)=2
=>x2*4-3+m-3=2
=>x2*4=2-m+6=8-m
=>x2=2-1/2m
=>x1=4-2+1/2m=1/2m+2
x1*x2=-m+3
=>-m+3=(1/2m+2)(2-1/2m)=4-1/4m^2
=>-m+3-4+1/4m^2=0
=>1/4m^2-m-1=0
=>m^2-4m-4=0
=>\(m=2\pm2\sqrt{2}\)

Để ĐTHS cắt cả 2 trục tọa độ \(\Rightarrow m\ne0\)
Khi đó ta có: giao điểm với trục hoành: \(mx+2=0\Rightarrow x=-\dfrac{2}{m}\)
Giao điểm với trục tung: \(y=m.0+2=2\)
a. \(A\left(-\dfrac{2}{m};0\right)\Rightarrow OA=\left|x_A\right|=\left|\dfrac{2}{m}\right|\)
\(B\left(0;2\right)\Rightarrow OB=\left|y_B\right|=2\)
\(OA=OB\Rightarrow\left|\dfrac{2}{m}\right|=2\Rightarrow m=\pm1\)
b. \(C\left(-\dfrac{2}{m};0\right);D\left(0;2\right)\Rightarrow\left\{{}\begin{matrix}OC=\left|\dfrac{2}{m}\right|\\OD=2\end{matrix}\right.\)
\(tanC=\dfrac{OD}{OC}=\left|m\right|=2\Rightarrow m=\pm2\)

a: Tọa độ A là:
y=0 và -2x+2=0
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
x=0 và y=-2x+2
=>x=0 và y=-2*0+2=2
=>B(0;2)
b: C thuộc Ox nên C(x;0)
D thuộc Oy nên D(0;y)
ABCD là hình thoi nên AB=AD và vecto AB=vecto DC
A(1;0); B(0;2); C(x;0); D(0;y)
\(\overrightarrow{AB}=\left(-1;2\right);\overrightarrow{DC}=\left(x;-y\right)\)
\(AB=\sqrt{\left(0-1\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(AD=\sqrt{\left(0-1\right)^2+\left(y-0\right)^2}=\sqrt{y^2+1}\)
vecto AB=vecto DC
=>x=-1 và -y=2
=>x=-1 và y=-2
AB=AD
=>y^2+1=5
=>y^2=4
=>y=2(loại) hoặc y=-2(nhận)
Vậy: x=-1 và y=-2
=>C(-1;0); D(0;-2)
Gọi phương trình (d2) có dạng là y=ax+b
(d2) đi qua C và D nên ta có hệ phương trình:
a*(-1)+b=0 và 0*a+b=-2
=>b=-2 và -a=-b=2
=>a=-2 và b=-2
=>y=-2x-2
c: (d1): y=-2x+2 và (d2): y=-2x-2
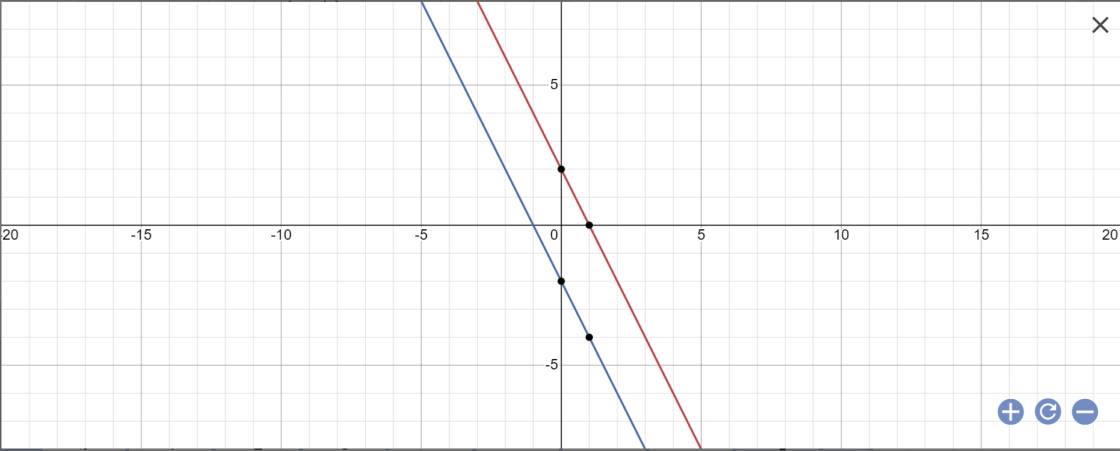
C. (M;5) tiếp xúc với Ox cắt Oy