Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tiêu điểm có tọa độ \((4;0)\) nên ta có \(p = 8\)
Suy ra phương trình chính tắc của parabol là: \({y^2} = 16x\)
b) Đường chuẩn có phương trình \(x = - \frac{1}{6}\), nên ta có \(p = - \frac{1}{3}\)
Suy ra phương trình chính tắc của parabol có dạng \({y^2} = - \frac{2}{3}x\)
c) Gọi phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm \((1;4)\) vào phương trình \({y^2} = 2px\) ta có:
\({4^2} = 2p.1 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)
d) Gọi \(F\left( {\frac{p}{2};0} \right)\), \(\Delta :x + \frac{p}{2} = 0\) lần lượt là tiêu điểm và phương trình đường chuẩn của parabol ta có:
\(d\left( {F,\Delta } \right) = \frac{{\left| {\frac{p}{2} + \frac{p}{2}} \right|}}{1} = 8 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)

Ta có:

Tổng khoảng cách từ 1 điểm thuộc Elip đến 2 tiêu điểm bẳng 2a= 5.
Chọn C.

a: Phương trình tổng quát là:
3(x-1)+1(y+3)=0
=>3x-3+y+3=0
=>3x+y=0
b: vecto AB=(-1;4)
Phương trình tham số của AB là:
\(\left\{{}\begin{matrix}x=1-t\\y=-3+4t\end{matrix}\right.\)
c: \(d\left(B;d\right)=\dfrac{\left|0\cdot3+1\cdot1\right|}{\sqrt{3^2+1^2}}=\dfrac{1}{\sqrt{10}}\)

Chọn A.
Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇔ a = 5, a 2 = 25
Độ dài tiêu cự bằng 6 ⇒ 2c = 6 ⇔ c = 3
Ta có: a 2 - b 2 = c 2 ⇒ b 2 = a 2 - c 2 = 5 2 - 3 2 = 16
Vậy phương trình của elip (E) là:
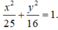

Ta có: độ dài trục lớn là 10 nên 2a= 10 => a= 5.
Độ dài tiêu cự là 6 nên 2c= 6 => c= 3
Ta có: b2 = a2- c2= 25- 9= 16 => b= 4
Vậy phương trình của Elip là: x 2 25 + y 2 16 = 1
Chọn A.

a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 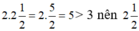 không là nghiệm của bất phương trình ,
không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 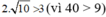 nên √10 không là nghiệm của bất phương trình,
nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: 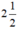 ; π; √10
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:


Đáp án A
Ta có tâm sai 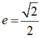
khoảng cách giữa hai đường chuẩn là:
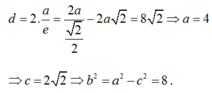
Suy ra phương trình elip là:
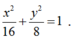

9x^2-3y^2=1
=>\(\dfrac{x^2}{\dfrac{1}{9}}-\dfrac{y^2}{\dfrac{1}{3}}=1\)
=>a=1/3; b=1/căn 3
\(c^2=b^2-a^2=\dfrac{1}{3}-\dfrac{1}{9}=\dfrac{2}{9}\)
=>\(c=\dfrac{\sqrt{2}}{3}\)
=>\(2c=\dfrac{2\sqrt{2}}{3}\)
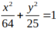
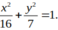
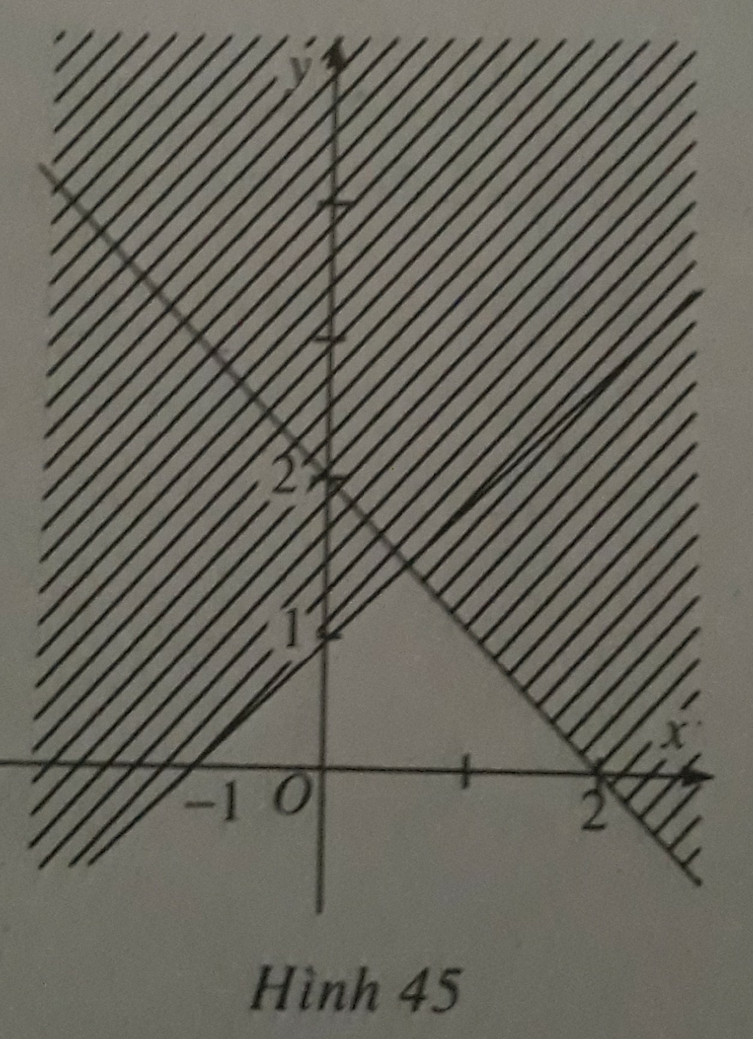
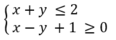 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.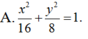
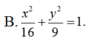
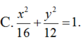
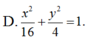
Ta có: Tiêu cự 2c= 6 => c= 3
Khoảng cách giữa 2 đường chuẩn .
2 a e = 50 3
=> 6a2= 50 c nên a2= 25 => b2= 16
Vậy phương trình (E) cần tìm là:
Chọn C.