Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
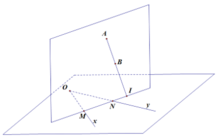
AB và mặt phẳng (Ox, Oy) luôn có điểm chung I
α chứa AB
⇒ I luôn nằm trên giao tuyến của α và (Ox, Oy) (1)
Ta lại có: α thay đổi cắt Ox tại M, Oy tại N
Xét α và (Ox, Oy) có M và N là điểm chung
⇒ MN là giao tuyến của 2 mặt phẳng (2)
(1);(2): M, N, I thẳng hàng
⇒ MN luôn đi qua I cố định

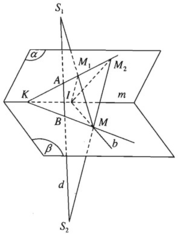
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.

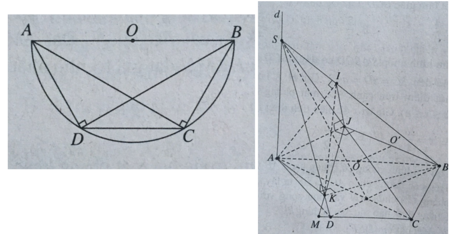
Nhận xét
Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.
Như vậy: ∠(ACB) = ∠(ADB) = 1v.
a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC
BC ⊥ SA & BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC. (1)
Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)
Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.
Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))
AJ ⊥ BC & AJ ⊥ SB (do SB ⊥ (P)) ⇒ AJ ⊥ (SBC) ⇒ AJ ⊥ JI (⊂ (SBC)) (3)
Lý luận tương tự, ta có:
BD ⊥ AD & BD ⊥ SA ⇒ BD ⊥ (SAD) ⇒ BD ⊥ AK (⊂ (SAD))
AK ⊥ BD & AK ⊥ SB(⊂ (P)) ⇒ AK ⊥ (SBD) ⇒ AK ⊥ KI. (4)
Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).
b) Ta có ngay O’ là trung điểm BJ
Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ
Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)
c) Ta có (SCD) ∩ (ABCD) = CD.
Gọi M = JK ∩ CD
SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)
SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)
Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.
Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.
d) ΔAIB vuông tại I nên OA = OB = OI
ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).
ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).
Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.
e) Theo chứng minh câu c.
f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).
Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn ( C 1 ) đường kính AB nằm trong mặt phẳng (B, d).
Tương tự, tập hợp J là đường tròn ( C 2 ) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).

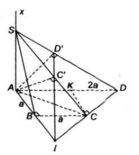
a) Ta có:
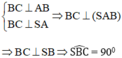
Gọi K là trung điểm của AD ta có CK = AB = AD/2 nên tam giác ACD vuông tại C
Ta có:
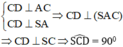
b) Trong mặt phẳng (SAC) vẽ AC’ ⊥ SC và trong mặt phẳng (SAD) vẽ AD’ ⊥ SD
Ta có AC’⊥ CD (vì CD ⊥ (SAC))
Và AC’ ⊥ SC nên suy ra AC’ ⊥ (SCD) ⇒ AC’ ⊥ SD
Ta lại có AB ⊥ AD và AB ⊥ SA nên AB ⊥ (SAD) ⇒ AB ⊥ SD
Ba đường thẳng AD’, AC’ và AB cùng đi qua điểm A và vuông góc với SD nên cùng nằm trong mặt phẳng (α) qua A và vuông góc với SD
c) Ta có C’D’ là giao tuyến của (α) với mặt phẳng (SCD). Do đó khi S di động trên tia Ax thì C’D’ luôn luôn đi qua một điểm cố định là giao điểm của AB và CD
AB ⊂ (α), CD ⊂ (SCD) ⇒ I ∈ (α) ∩ (SCD) = C’D’

*Tìm giao tuyến của 2 mặt phẳng (M,a) và (M,b):
Có M là một điểm chung
Theo bài : a và b cắt nhau tại O
=> O thuộc a ⊂ (M,a) =>O thuộc (M,a)
và O thuộc b ⊂ (M,b) =>O thuộc (M,b)
=>O là điểm chung thứ hai
Vậy: (M,a) ∩ (M,b) = OM
Do đó giao tuyến OM lun thuộc mặt phẳng tạo bởi c và O ( mp (O,c)) là một mp cố định.

Dễ thấy P là điểm chính giữa nên D,N,P thẳng hàng
Cần chứng minh
Ta có :
b) Theo câu a suy ra
Mà cân tại I ( do IP = ID ) nên
Suy ra
c) từ câu b ( 1 )
Theo hệ thức lượng, ta có :
Do đó :
Suy ra ( 2 )
Từ ( 1 ) và ( 2 ) kết hợp với IM // PN suy ra A,M,N thẳng hàng
Gọi \(\overrightarrow{u},\overrightarrow{v}\) theo thứ tự là vec tơ chỉ phương đơn vị của các tia Ox, Oy, tương ứng cùng hướng với các tia Ox, Oy gọi I là tâm của \(\omega\). Chọn O làm gốc vec tơ điểm và với mỗi điểm X của mặt phẳng, ký hiệu \(\overrightarrow{x}\) để chỉ vec tơ \(\overrightarrow{OX}\). Trung trực OA cắt các đường thẳng \(d_1,d_2\) theo thứ tự tại B, C.
Khi đó B, C cố định và do I nằm trên đường thẳng BC nên \(\overrightarrow{i}=\alpha\overrightarrow{b}+\left(1-\alpha\right)\overrightarrow{c}\)
Mặt khác , theo định lí chiếu ta có :
\(\overrightarrow{m}=2\left(\overrightarrow{i}.\overrightarrow{u}\right).\overrightarrow{u}\) và \(\overrightarrow{n}=2\left(\overrightarrow{i}.\overrightarrow{v}\right).\overrightarrow{v}\)
Gọi P là trung điểm MN. Suy ra \(2\overrightarrow{p}=\overrightarrow{m}.\overrightarrow{n}\). Bởi vậy, với \(b=OB,c=OC\) và \(t=\cos<\left(\overrightarrow{u}\overrightarrow{v}\right)\) thì b, c, t là các hằng số và :
\(\overrightarrow{p}=\left[\alpha.\overrightarrow{b}\overrightarrow{u}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{u}\right].\overrightarrow{u}+\left[\alpha.\overrightarrow{b}\overrightarrow{v}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{v}\right].\overrightarrow{v}\)
\(=\alpha.b\left(\overrightarrow{u}+t\overrightarrow{v}\right)+\left(1-\alpha\right).c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\)
\(=\alpha\overrightarrow{x}+\left(1-\alpha\right)\overrightarrow{y}\)
Trong đó \(\overrightarrow{x}=\overrightarrow{OX}=b\left(\overrightarrow{u}+t\overrightarrow{v}\right)\) và \(\overrightarrow{y}=\overrightarrow{OY}=c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\) là các vec tơ cố định
Suy ra P luôn nằm trên đường thẳng XY cố định khi \(\omega\) thay đổi