Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.

Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn

Lời giải:
Đường thẳng $(d_1)$ có VTPT $(2,-4)$
$\Rightarrow$ VTCP của $(d_1)$: $(4,2)$
VTCP của $(d_2)$: $(m, -m-1)$
Để $(d_1), (d_2)$ vuông góc với nhau khi chỉ khi 2 VTCP của 2 đường thẳng vuông góc với nhau
$\Leftrightarrow 4m+2(-m-1)=0$
$\Leftrightarrow m=1$

a. Tọa độ A thỏa mãn:
\(4-3t+2\left(-1+2t\right)-1=0\Rightarrow t=-1\)
\(\Rightarrow A\left(7;-3\right)\)
b. d1 nhận \(\left(-3;2\right)=-1\left(3;-2\right)\) là 1 vtcp nên đường thẳng d nhận \(\left(2;3\right)\) là 1 vtcp và \(\left(3;-2\right)\) là 1 vtpt
Phương trình tham số d: \(\left\{{}\begin{matrix}x=7+2t\\y=-3+3t\end{matrix}\right.\)
Pt tổng quát:
\(3\left(x-7\right)-2\left(y+3\right)=0\Leftrightarrow3x-2y-27=0\)
Đường thẳng d2 nhận \(\left(1;2\right)\) là 1 vtpt nên d3 nhận \(\left(1;2\right)\) là 1 vtpt và \(\left(2;-1\right)\) là 1 vtcp
Phương trình tham số d3: \(\left\{{}\begin{matrix}x=7+2t\\y=-3-t\end{matrix}\right.\)
Pt tổng quát:
\(1\left(x-7\right)+2\left(y+3\right)=0\Leftrightarrow x+2y-1=0\)

Cho 2 đường thẳng cắt nhau d 1 : a 1 x + b 1 y + c 1 = 0 v à d 2 : a 2 x + b 2 y + c 2 = 0 .
Lấy điểm M(x, y) bất kì trên đường phân giác của góc tạo bởi 2 đường thẳng d1; d2.
Theo tính chất đường phân giác của góc ta có:
d ( M ; d 1 ) = d ( M ; d 2 ) ⇔ a 1 x + b 1 y + c 1 a 1 2 + b 1 2 = a 2 x + b 2 y + c 2 a 2 2 + b 2 2 ⇔ a 1 x + b 1 y + c 1 a 1 2 + b 1 2 = ± a 2 x + b 2 y + c 2 a 2 2 + b 2 2
ĐÁP ÁN B
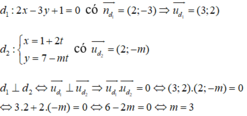
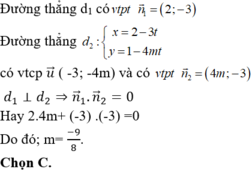
\(\left\{{}\begin{matrix}x=4+2t\\y=1-5t\end{matrix}\right.\)
Vậy: VTCP là (2;-5) và điểm mà (d1) đi qua là A(4;1)
=>VTPT là (5;2)
Phương trình đường thẳng của (d1) là:
5(x-4)+2(y-1)=0
=>5x-20+2y-2=0
=>5x+2y-22=0
(d2): 2x-5y-14=0
=>(d1) và (d2) vuông góc