
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
Hàm số đồng biến trên R khi:
\(m-5>0\Rightarrow m>5\)
3.
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{12}{15}=0,8\)

\(\dfrac{1}{\sqrt[3]{16}+\sqrt[3]{12}+\sqrt[3]{9}}=\dfrac{1}{\left(\sqrt[3]{4}\right)^2+\sqrt[3]{4}.\sqrt[3]{3}+\left(\sqrt[3]{3}\right)^2}\)
\(=\dfrac{\left(\sqrt[3]{4}-\sqrt[3]{3}\right)}{\left(\sqrt[3]{4}-\sqrt[3]{3}\right)\left(\sqrt[3]{4}\right)^2+\sqrt[3]{4}.\sqrt[3]{3}+\left(\sqrt[3]{3}\right)^2}\)
\(=\dfrac{\sqrt[3]{4}-\sqrt[3]{3}}{\left(\sqrt[3]{4}\right)^3-\left(\sqrt[3]{3}\right)^3}=\dfrac{\sqrt[3]{4}-\sqrt[3]{3}}{4-3}=\sqrt[3]{4}-\sqrt[3]{3}\)

a) \(\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}\)
\(=\sqrt{\dfrac{\left(3-\sqrt{5}\right)^2}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}}\)
\(=\dfrac{\sqrt{\left(3-\sqrt{5}\right)^2}}{\sqrt{3^2-\left(\sqrt{5}\right)^2}}\)
\(=\dfrac{\left|3-\sqrt{5}\right|}{\sqrt{9-5}}\)
\(=\dfrac{3-\sqrt{5}}{2}\)
b) \(\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}\)
\(=\sqrt{\dfrac{\left(2-\sqrt{3}\right)^2}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}}\)
\(=\dfrac{\sqrt{\left(2-\sqrt{3}\right)^2}}{\sqrt{2^2-\left(\sqrt{3}\right)^2}}\)
\(=\dfrac{\left|2-\sqrt{3}\right|}{\sqrt{4-3}}\)
\(=\dfrac{2-\sqrt{3}}{1}\)
\(=2-\sqrt{3}\)
a: \(=\sqrt{\dfrac{\left(3-\sqrt{5}\right)\left(3-\sqrt{5}\right)}{4}}=\dfrac{3-\sqrt{5}}{2}\)
b: \(=\sqrt{\dfrac{\left(2-\sqrt{3}\right)^2}{1}}=2-\sqrt{3}\)
d: \(=\left(-3+3\sqrt{6}+4+2\sqrt{6}-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
=(căn 6-11)(căn 6+11)
=6-121=-115

e: \(\dfrac{3\sqrt{5}-2\sqrt{2}}{2\sqrt{5}-3\sqrt{2}}=\dfrac{18+5\sqrt{10}}{2}\)

72: \(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}=a-\sqrt{ab}+b\)

`= ((1-sqrta)(1-sqrta))/((sqrta+1)(sqrta-1))`
`=-(1-2 sqrt a +a)/(a-1)``




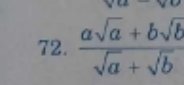 trục căn thức ở mẫu
trục căn thức ở mẫu 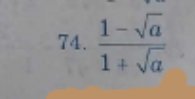 trục căn thức ở mẫu
trục căn thức ở mẫu
\(\dfrac{1+3\sqrt{2}-2\sqrt{3}}{\sqrt{6}+\sqrt{3}+\sqrt{2}}\)
\(=\dfrac{\left[1+\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)\right]\left[\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right]}{\left[\sqrt{6}+\left(\sqrt{3}+\sqrt{2}\right)\right]\left[\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right]}\)
Tử:
\(\left[1+\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)\right]\left[\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right]\)
\(=\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)+6\left(\sqrt{3}-\sqrt{2}\right)-\sqrt{6}\) (nhân phân phối)
\(=5\sqrt{3}-7\sqrt{2}\)
Mẫu:
\(\left[\sqrt{6}+\left(\sqrt{3}+\sqrt{2}\right)\right]\left[\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right]\)
\(=6-\left(5+2\sqrt{6}\right)\)
\(=1-2\sqrt{6}\)
Ta có:
\(\dfrac{5\sqrt{3}-7\sqrt{2}}{1-2\sqrt{6}}\)
\(=\dfrac{\left(5\sqrt{3}-7\sqrt{2}\right)\left(1+2\sqrt{6}\right)}{1-24}\)
\(=\dfrac{5\sqrt{3}+30\sqrt{2}-7\sqrt{2}-28\sqrt{3}}{-23}\)
\(=\dfrac{-23\left(\sqrt{3}-\sqrt{2}\right)}{-23}\)
\(=\sqrt{3}-\sqrt{2}\)