Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(2x^3-3x^2-5x=0\)
\(x\left(x+1\right)\left(2x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(L\right)\\x=-1\left(TM\right)\\x=\dfrac{5}{2}\left(L\right)\end{matrix}\right.\)
\(A=\left\{-1\right\}\)
b) \(x< \left|3\right|\)\(\Leftrightarrow-3< x< 3\)
\(B=\left\{-2;-1;1;2\right\}\)
c) \(C=\left\{-3;3;6;9\right\}\)
a) \(A=\left\{x\in Z|2x^3-3x^2-5x=0\right\}\)
\(2x^3-3x^2-5x=0\)
\(\Leftrightarrow x\left(2x^2-3x-5\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(2x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=\dfrac{5}{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow A=\left\{0;-1\right\}\)
b) \(B=\left\{-2;-1;0;1;2\right\}\)
c) \(C=\left\{-3;3;6;9\right\}\)

a: x+2<=1
=>x<=-1
=>E={;...;-2;-1}
b: 3<n^2<30
mà n thuộc N
nên \(n^2\in\left\{4;9;16;25\right\}\)
=>\(F=\left\{2;3;4;5\right\}\)
g: -4<x<12
mà x chia hết cho 3(x=3k; k nguyên)
nên \(x\in\left\{-3;0;3;6;9\right\}\)
=>G={-3;0;3;6;9}

| k | 0 | 1 | 2 | 3 | 4 | 5 |
| 3k – 2 | -2 | 1 | 4 | 7 | 10 | 13 |
Do đó: A = {-2, 1, 4, 7, 10, 13}.

a: A={0;1;2;3}
b: B={-16;-13;-10;-7;-4;-1;2;5;8}
c: C={-9;-8;-7;...;7;8;9}
d: \(D=\varnothing\)

\(c,20=2^2\cdot5\\ 45=3^2\cdot5\\ ƯCLN\left(20,45\right)=5\\ \RightarrowƯC\left(20,45\right)=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\\ C=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\)
\(d,\left(6x^2-7x+1\right)\left(x^3-x\right)=0\\ \Leftrightarrow\left(x-1\right)\left(6x-1\right)x\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=0\\x=\dfrac{1}{6}\\x=1\\x=-1\end{matrix}\right.\)
\(\Leftrightarrow D=\left\{-1;0;\dfrac{1}{6};1\right\}\)
Sửa: \(\left[{}\begin{matrix}x=0\\x=\dfrac{1}{6}\\x=1\\x=-1\end{matrix}\right.\Leftrightarrow D=\left\{-1;0;\dfrac{1}{6};1\right\}\)

i: I={-5;-4;-3;-2;-1;0;1;2;3;4;5}
j: B={0;4;8;12;16;20;24;28}

\(\left(2x+1\right)\left(x^2+x-1\right)\left(2x^2-3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x^2+x-1=0\\2x^2-3x+1=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\\x=\dfrac{1}{2}\end{matrix}\right.\) (pt \(x^2+x-1=0\) ko có nghiệm hữu tỉ nên ko cần quan tâm)
\(A=\left\{-\dfrac{1}{2};\dfrac{1}{2};1\right\}\)
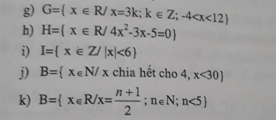
\(G=\left\{X\inℤ|X=\frac{3k-2}{k+1},k\inℤ\right\}\)
\(G=\left\{2;4;-2;8\right\}\)