Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\dfrac{\sqrt{ab}}{b}+\sqrt{\dfrac{a^2b}{b^2a}}=\dfrac{\sqrt{ab}}{b}+\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{ab}}{b}+\dfrac{\sqrt{ab}}{b}=\dfrac{2\sqrt{ab}}{b}\left(B\right)\)

Lời giải:
Từ $a+b> c\Rightarrow a+b-c>0$ (cái này hiển nhiên)
Từ $|a-b|< c\Leftrightarrow |a-b|^2< c^2$
$\Leftrightarrow (a-b)^2< c^2$
$\Leftrightarrow (a-b-c)(a-b+c)<0$
Với $c>0$ thì $a-b-c< a-b+c$ nên để tích âm thì $a-b-c<0< a-b+c$
Hay $a-b-c<0$ và $a-b+c>0$

\(1,a+b+c=0\Leftrightarrow a=-b-c\Leftrightarrow a^2=b^2+2bc+c^2\Leftrightarrow b^2+c^2=a^2-2bc\)
Tương tự: \(\left\{{}\begin{matrix}a^2+b^2=c^2-2ab\\c^2+a^2=b^2-2ac\end{matrix}\right.\)
\(\Leftrightarrow N=\dfrac{a^2}{a^2-a^2+2bc}+\dfrac{b^2}{b^2-b^2+2ca}+\dfrac{c^2}{c^2-c^2+2ac}\\ \Leftrightarrow N=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2bc}=\dfrac{a^3+b^3+c^3}{2abc}=\dfrac{a^3+b^3+c^3-3abc+3abc}{2abc}\\ \Leftrightarrow N=\dfrac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+3abc}{2abc}\\ \Leftrightarrow N=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)

xí câu 1:))
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\frac{x^2}{y-1}+\frac{y^2}{x-1}\ge\frac{\left(x+y\right)^2}{x+y-2}\)(1)
Đặt a = x + y - 2 => a > 0 ( vì x,y > 1 )
Khi đó \(\left(1\right)=\frac{\left(a+2\right)^2}{a}=\frac{a^2+4a+4}{a}=\left(a+\frac{4}{a}\right)+4\ge2\sqrt{a\cdot\frac{4}{a}}+4=8\)( AM-GM )
Vậy ta có đpcm
Đẳng thức xảy ra <=> a=2 => x=y=2

Ta có : \(\frac{a^2-bc}{a}+\frac{b^2-ac}{b}+\frac{c^2-ab}{c}=0\)
=> \(a-\frac{bc}{a}+b-\frac{ac}{b}+c-\frac{ab}{c}=0\)
=> \(a+b+c=\frac{bc}{a}+\frac{ac}{b}+\frac{ab}{c}\)
=> \(a+b+c=abc\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)
=> \(\frac{a+b+c}{abc}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)
=> \(\frac{1}{bc}+\frac{1}{ac}+\frac{1}{ab}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)
=> \(\frac{2}{bc}+\frac{2}{ac}+\frac{2}{ab}=\frac{2}{a^2}+\frac{2}{b^2}+\frac{2}{c^2}\)
=> \(\frac{2}{a^2}+\frac{2}{b^2}+\frac{2}{c^2}-\frac{2}{bc}-\frac{2}{ac}-\frac{2}{ac}=0\)
=> \(\left(\frac{1}{a^2}-\frac{2}{ab}+\frac{1}{b^2}\right)+\left(\frac{1}{a^2}-\frac{2}{ac}+\frac{1}{c^2}\right)+\left(\frac{1}{b^2}-\frac{1}{bc}+\frac{1}{c^2}\right)=0\)
=> \(\left(\frac{1}{a}-\frac{1}{b}\right)^2+\left(\frac{1}{a}-\frac{1}{c}\right)^2+\left(\frac{1}{b}-\frac{1}{c}\right)^2=0\)
=> \(\hept{\begin{cases}\frac{1}{a}-\frac{1}{b}=0\\\frac{1}{a}-\frac{1}{c}=0\\\frac{1}{b}-\frac{1}{c}=0\end{cases}}\Rightarrow\hept{\begin{cases}\frac{1}{a}=\frac{1}{b}\\\frac{1}{a}=\frac{1}{c}\\\frac{1}{b}=\frac{1}{c}\end{cases}}\Rightarrow\frac{1}{a}=\frac{1}{b}=\frac{1}{c}\Rightarrow a=b=c\left(\text{đpcm}\right)\)

a/
\(=\frac{a+b}{b^2}.\frac{\left|a\right|.b^2}{\left|a+b\right|}=\frac{\left(a+b\right).b^2.\left|a\right|}{b^2\left(a+b\right)}=\left|a\right|\)
b/
\(=\frac{\left(\sqrt{a}+\sqrt{b}\right)^2}{2\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}-\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{2\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{4b}{2\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\frac{4\sqrt{ab}+4b}{2\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{2\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}\)


a) \(2\sqrt{5a^2}=2\sqrt{5}\left|a\right|=-2a\sqrt{5}\)
b)\(2\sqrt{18a^2}=2.3\sqrt{2}.\left|a\right|=6a\sqrt{2}\)
c)\(\sqrt{-9b^3}=\sqrt{9.\left(-b\right)^3}=3\sqrt{-b}.\left|b\right|=-3b\sqrt{-b}\)
d)\(\sqrt{24a^4b^8}=\sqrt{6.\left(4a^2b^4\right)^2}=2a^2b^4\sqrt{6}\)
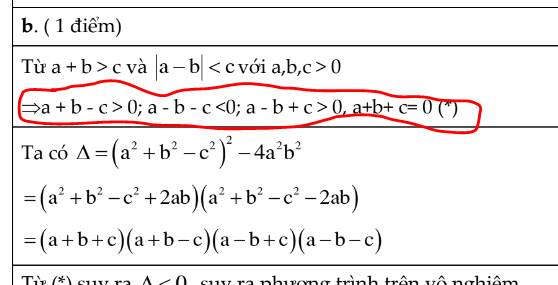
Đáp án là B