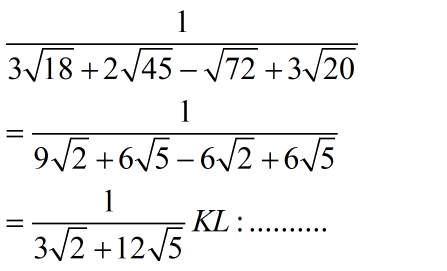\(\dfrac{1}{3}\sqrt{18}+2\sqrt{45}-\sqrt{72}+3\sqrt{20}\)

\(=\dfrac{1}{3}\sqrt{9\times2}+2\sqrt{9\times5}-\sqrt{9\times8}+3\sqrt{4\times5}\)

\(=\sqrt{2}+6\sqrt{5}-6\sqrt{2}+6\sqrt{5}\) \(=12\sqrt{5}-5\sqrt{2}\)

toan la toan chu ko phai phim hoat hinh

ý của nhất sông núi là sao?

HELP ME♥

\(\sqrt{x+72}=72-x^2\Rightarrow x+72=72^2-144x^2+x^4\Rightarrow0=5184-72+x^4-144x^2-x=5112+x^4-144x^2-x\) =>\(0=x^4-9x^3+9x^3-81x^2-63x^2+567x-568x+5112\)

=>\(0=\left(x-9\right)\left(x^3+9x^2-63x-568\right)\)

=>\(0=\left(x-9\right)\left(x+8\right)\left(x^2+x-71\right)\)=>x=9 hoac x=-8

Ta có :

\(a^2=72+\sqrt{72+\sqrt{72+\sqrt{72+.......}}}\)

\(\Leftrightarrow a^2=72+a\Leftrightarrow a^2-a-72=0\Leftrightarrow\left(a-9\right)\left(a+8\right)=0\)

\(\Rightarrow\orbr{\begin{cases}a=9\\a=-8\end{cases}}\)

Mà a > 0 nên a = 9 \(\Rightarrow\left[a\right]=9\)

\(72=x+\sqrt{72}\)

\(\Leftrightarrow x=72-\sqrt{72}\)

\(\Leftrightarrow x=72-6\sqrt{2}\)

\(72=x+\sqrt{72}\)

\(\Rightarrow x=72-\sqrt{72}\)

\(\Rightarrow x=72-\sqrt{36.2}\)

\(\Rightarrow x=72-\sqrt{36}.\sqrt{2}\)

\(\Rightarrow x=72-6\sqrt{2}\)

căn (40-x)=a , căn (45-x)=b,căn(72-x)=c (a,b,c >=0 )

đưa về hệ: ab+bc+ca=40-a^2 -> ab+bc+ca+a^2=40 

                 ab+bc+ca=45-b^2......

                 ab+bc+ca=72-c^2.....

đến đó ok rồi