Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng ( - ∞ ; m), (m; + ∞ ) khi và chỉ khi:
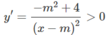
⇔ − m 2 + 4 > 0
⇔ m 2 < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3

\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)

Đáp án: D.
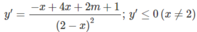
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3

Chọn B.
Tập xác định ![]()
Có 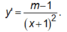
Hàm số nghịch bến trên mỗi khoảng của tập xác định
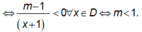

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

\(y'=3x^2-6mx\)
Hàm nghịch biến trên \(\left(0;1\right)\) khi với mọi \(x\in\left(0;1\right)\) ta có:
\(3x^2-6mx\le0\)
\(\Leftrightarrow3x\left(x-2m\right)\le0\)
\(\Leftrightarrow x-2m\le0\)
\(\Leftrightarrow m\ge\max\limits_{\left(0;1\right)}\dfrac{x}{2}\Rightarrow m\ge\dfrac{1}{2}\)
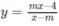 đồng biến trên từng khoảng xác định;
đồng biến trên từng khoảng xác định;

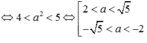
Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3