Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

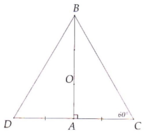
Ba đường thẳng AM, BN, CP lần lượt vuông góc với ba cạnh BC, AC, AB của tam giác và chúng giao nhau tại một điểm.

a) lấy D là trung điểm đoạn AB.
Kẻ đường thẳng qua D và vuông góc với AB, ta được trung trực đoạn AB.
b) lấy E là trung điểm đoạn BC.
Kẻ đường thẳng qua E và vuông góc với BC, ta được trung trực đoạn BC.
c) Hai trung trực trên cắt nhau tại tâm O của đường tròn (O)

Câu c chỉ cần kéo xuống và nói là cái điểm giao nhau là trwc tâm nên BH vuông góc OC ..... Còn ta có thể thấy là tam giác BOC là tam giác cân tại B nên AC=OM mà HA=HM nên HO=HC => đó là tam giác cân tại H
Bạn tự vẽ hình nha![]()
a.
Xét tam giác ABH vuông tại A và tam giác MBH vuông tại M có:
BH là cạnh chung
HBA = HBM (BH là tia phân giác của ABM)
=> Tam giác ABH = Tam giác MBH (cạnh huyền - góc nhọn)
b.
- AH = MH (tam giác ABH = tanm giác MBH) => H thuộc đường trung trực của AM
- AB = MB (tam giác ABH = tam giác MBH) => B thuộc đường trung trực của AM
=> BH là đường trung trực của AM
c.
- CA là đường cao của tam giác BOC
- OM là đường cao của tam giác BOC
=> H là trực tâm của tam giác BOC.
=> BH là đường cao của tam giác BOC
hay BH _I_ OC
Xét tam giác AHO và tam giác MHC có:
OHA = CHM (2 góc đối đỉnh)
AH = MH (tam giác ABH = tam giác MBH)
OAH = CMH ( = 90 )
=> Tam giác AHO = Tam giác MHC (g.c.g)
BO = BA + AO
BC = BM + MC
mà BA = BM (tam giác ABH = tam giác MBH)
AO = MC (tam giác AHO = tam giác MHC)
=> BO = BC
=> Tam giác BOC cân tại B
Chúc bạn học tốt![]()

Bài làm ai trên 11 điểm tích mình thì mình tích lại
Ông tùng hơn tùng số tuổi là :
29 + 32 = 61 (tuổi )
Vậy ông của tùng hơn tùng 61 tuổi

c: Đường trung trực của hai đoạn nói trên giao nhau tại O

3 dường này đồng quy tại tâm đường tròn ngoại tiếp của tam giác
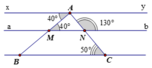



a) Vì x A M ^ = A M N ^ = 40 0 , mà hai góc này ở vị trí so le trong nên xy // MN (1)
Gọi đường thẳng chứa đoạn MN là ab
Ta có:
A N b ^ + A N M ^ = 180 0 ⇒ 130 0 + A N M ^ = 180 0 ⇒ A N M ^ = 180 0 − 130 0 ⇒ A N M ^ = 50 0
Vì A N M ^ = A C B ^ = 50 0 , mà hai góc này ở vị trí đồng vị nên MN // BC (2)
Từ (1) và (2) suy ra xy // MN // BC
b) Vì xy // MN nên x A N ^ = A N b ^ = 130 0 (hai góc so le trong)
Tia AM nằm giữa hai tia Ax và AN nên x A M ^ + M A N ^ = x A N ^ = 130 0
⇒ M A N ^ = 130 0 − 40 0 = 90 0 hay B A C ^ = 90 0
Vì MN // BC nên A B C ^ = A M N ^ = 40 0 (hai góc đồng vị)