Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Với \(m=0\) hàm ko có tiệm cận
- Với \(m< 0\Rightarrow\) miền xác định của hàm số ko chứa vô cực \(\Rightarrow\) ĐTHS ko có tiệm cận ngang
- Với \(m>0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x}{\sqrt{mx^2+1}}=\lim\limits_{x\rightarrow-\infty}\dfrac{1}{-\sqrt{m+\dfrac{1}{x^2}}}=-\dfrac{1}{\sqrt{m}}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x}{\sqrt{mx^2+1}}=\lim\limits_{x\rightarrow+\infty}\dfrac{1}{\sqrt{m+\dfrac{1}{x^2}}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) ĐTHS có 2 TCN khi \(m>0\)

\(y=\frac{\left(a-2b\right)x^2+bx+1}{x^2+x-b}\)
Nếu \(a-2b\ne0\Rightarrow\lim\limits_{x\rightarrow\infty}\frac{\left(a-2b\right)x^2+bx+1}{x^2+x-b}=a-2b\ne0\) \(\Rightarrow y=0\) ko phải TCN (loại)
\(\Rightarrow a-2b=0\)
Do hàm số có TCĐ \(x=1\Rightarrow\) phương trình \(x^2+x-b=0\) có nghiệm \(x=1\)
\(\Rightarrow1+1-b=0\Rightarrow b=2\Rightarrow a=4\)
\(\Rightarrow a+2b=8\)

Câu đầu tìm m để ĐTHS làm sao bạn?
2.
\(x=1\) là TCĐ của ĐTHS \(\frac{mx^2-3x}{x-1}=0\) khi và chỉ khi \(mx^2-3x=0\) không có nghiệm \(x=1\)
\(\Leftrightarrow m.1^2-3.1\ne0\Leftrightarrow m\ne3\)
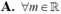
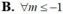
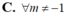
Đáp án C