Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a.
\(\left\{\begin{matrix} x\neq 0\\ 2x-1\geq 0\\ x^2-3x+2=(x-1)(x-2)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ x\geq \frac{1}{2}\\ x\neq 1; x\neq 2\end{matrix}\right.\)
$\Leftrightarrow x\geq \frac{1}{2}; x\neq 1; x\neq 2$
b. \(\left\{\begin{matrix}
x^2-1=(x-1)(x+1)\neq 0\\
7-2x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\neq \pm 1\\
x\leq \frac{7}{2}\end{matrix}\right.\)
c.
\(\left\{\begin{matrix} x\neq 0\\ 4-2x+x^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ (x-1)^2+3\neq 0\end{matrix}\right.\Leftrightarrow x\neq 0\)
d.
\(\left\{\begin{matrix} 25-x^2=(5-x)(5+x)\geq 0\\ x\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -5\leq x\leq 5\\ x\geq 0\end{matrix}\right.\Leftrightarrow 0\leq x\leq 5\)
a) \(y=\dfrac{1}{x}-\dfrac{\sqrt[]{2x-1}}{x^2-3x+2}\)
Điều kiện \(\) \(2x-1\ge0;x\ne0;x^2-3x+2\ne0\)
\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;\left(x-1\right)\left(x-2\right)\ne0\)
\(\Leftrightarrow x\ge\dfrac{1}{2};x\ne0;x\ne1;x\ne2\)

e: \(f\left(-x\right)=\dfrac{\left(-x\right)^4+3\cdot\left(-x\right)^2-1}{\left(-x\right)^2-4}=\dfrac{x^4+3x^2-1}{x^2-4}=f\left(x\right)\)
Vậy: f(x) là hàm số chẵn
\(c,f\left(-x\right)=\sqrt{-2x+9}=-f\left(x\right)\)
Vậy hàm số lẻ
\(d,f\left(-x\right)=\left(-x-1\right)^{2010}+\left(1-x\right)^{2010}\\ =\left[-\left(x+1\right)\right]^{2010}+\left(x-1\right)^{2010}\\ =\left(x+1\right)^{2010}+\left(x-1\right)^{2010}=f\left(x\right)\)
Vậy hàm số chẵn
\(g,f\left(-x\right)=\sqrt[3]{-5x-3}+\sqrt[3]{-5x+3}\\ =-\sqrt[3]{5x+3}-\sqrt[3]{5x-3}=-f\left(x\right)\)
Vậy hàm số lẻ
\(h,f\left(-x\right)=\sqrt{3-x}-\sqrt{3+x}=-f\left(x\right)\)
Vậy hàm số lẻ

a) y xác định \(\Leftrightarrow2x^2-5x+2\ne0\Leftrightarrow\left(x-2\right)\left(2x-1\right)\ne0\Leftrightarrow\left\{{}\begin{matrix}x-2\ne0\\2x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne\frac{1}{2}\end{matrix}\right.\). Vậy tập xác định D = R / { 2; 1/2}
b) y xác định \(\Leftrightarrow\left\{{}\begin{matrix}x-1\ne0\\2x+4\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ge-2\end{matrix}\right.\).
Vậy tập xác định D = \([-2;+\infty)/1\)
y xác định \(\Leftrightarrow x^2-3x+m-1\ne0\forall x\in R\)
suy ra phương trình x2 - 3x + m - 1 = 0 vô nghiệm
\(\Rightarrow\Delta=9-4\left(m-1\right)< 0\Leftrightarrow9-4m+4< 0\Leftrightarrow m>\frac{13}{4}\)
\(\Rightarrow m\in\left(\frac{13}{4};+\infty\right)\)

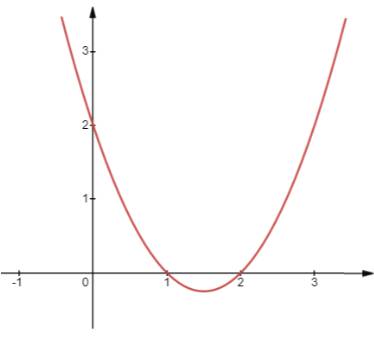
a) Đồ thị \(y = {x^2} - 3x + 2\)
- Có đỉnh là điểm \(I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{3}{2}\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;2);(1;0)
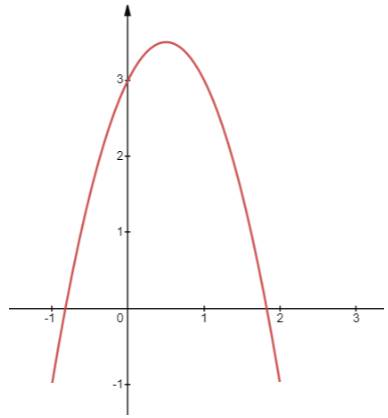
b) Đồ thị \(y = - 2{x^2} + 2x + 3\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{7}{2}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 2 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;3);(1;3)
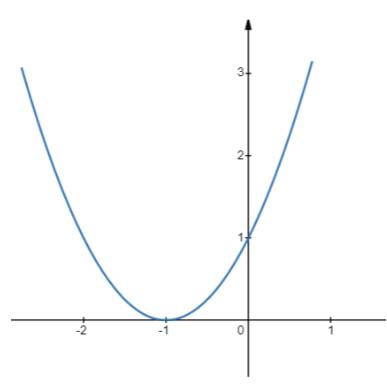
c) Đồ thị\(y = {x^2} + 2x + 1\)
- Có đỉnh là điểm \(I( - 1;0)\), có trục đối xứng là đường thẳng \(x = - 1\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;1); (1;4)
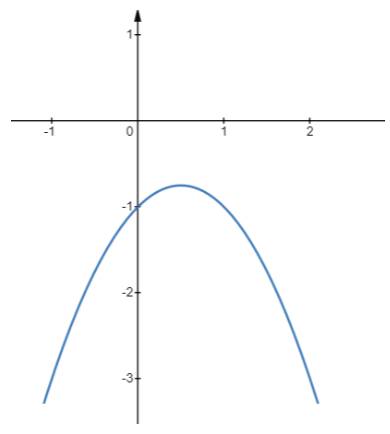
d) Đồ thị \(y = - {x^2} + x - 1\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{{ - 3}}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 1 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;-1); (1;-1)

Quy tắc xét tính chẵn lẻ của hàm số:
Chẵn \(\Leftrightarrow\left\{{}\begin{matrix}x\in D\Rightarrow-x\in D\\f\left(x\right)=f\left(-x\right)\end{matrix}\right.\)
Lẻ \(\Leftrightarrow\left\{{}\begin{matrix}x\in D\Rightarrow-x\in D\\f\left(x\right)=-f\left(-x\right)\end{matrix}\right.\)
a/ \(g=2x^4-x^2+5\)
\(x\in D=R\Rightarrow-x\in D\)
\(g\left(-x\right)=2\left(-x\right)^4-\left(-x\right)^2+5=2x^4-x^2+5=g\left(x\right)\)
=> hàm số chẵn
b/ \(y=x^3+3x\)
\(x\in D=R\Rightarrow-x\in D\)
\(y\left(-x\right)=\left(-x\right)^3+3\left(-x\right)=-x^3-3x=-\left(x^3+3x\right)\)
\(\Rightarrow y\left(x\right)=-y\left(-x\right)\)
=> hàm số lẻ
c/ \(y=x^3+3x+1\)
\(x\in D=R\Rightarrow-x\in D\)
\(y\left(-x\right)=\left(-x\right)^3+3\left(-x\right)+1=-x^3-3x+1\)
\(\Rightarrow\left\{{}\begin{matrix}y\left(x\right)\ne y\left(-x\right)\\y\left(x\right)\ne-y\left(-x\right)\end{matrix}\right.\)
=> hàm số ko chẵn ko lẻ
d/ \(y=x^4-3\)
\(x\in D=R\Rightarrow-x\in D\)
\(y\left(-x\right)=\left(-x\right)^4-3=x^4-3=y\left(x\right)\)
=> hàm số chẵn
e/ \(y=3x^4-\left|x\right|+2\)
\(x\in D=R\Rightarrow-x\in D\)
\(y\left(-x\right)=3\left(-x\right)^4-\left|-x\right|+2=3x^4-\left|x\right|+2=y\left(x\right)\)
=> hàm số chẵn
f/ \(x\in D=R\Rightarrow-x\in D\)
\(y\left(-x\right)=\left|-x-1\right|+\left|-x+1\right|=\left|x+1\right|+ \left|x-1\right|=y\left(x\right)\)
=> hàm số chẵn
Các câu sau làm tương tự
a/ \(g\left(-x\right)=2\left(-x\right)^4-\left(-x\right)^2+5=2x^4-x^2+5=g\left(x\right)\)
Hàm chẵn
b/ \(y\left(-x\right)=\left(-x\right)^3+3\left(-x\right)=-x^3-3x=-\left(x^3+3x\right)=-y\left(x\right)\)
Hàm lẻ
c/ \(y\left(-x\right)=-x^3-3x+1\)
Hàm ko chẵn ko lẻ
d/ \(y\left(-x\right)=x^4-3=y\left(x\right)\) hàm chẵn
e/ \(y\left(-x\right)=3x^4-\left|x\right|+2=y\left(x\right)\) hàm chẵn
f/ \(y\left(-x\right)=\left|-x-1\right|+\left|-x+1\right|=\left|x+1\right|+\left|x-1\right|=y\left(x\right)\)
Hàm chẵn
g/ \(y\left(-x\right)=\left|-x-1\right|-\left|-x+1\right|=\left|x+1\right|-\left|x-1\right|=-y\left(x\right)\)
Hàm lẻ
h/ Hàm ko chẵn ko lẻ
a)\(-2x^3+3x=x\left(x-\frac{\sqrt{6}}{2}\right)\left(x+\frac{\sqrt{6}}{2}\right)\)
Lập bảng biến thiên với các khoảng (\(-\infty;\frac{-\sqrt{6}}{2}\)];(\(\frac{-\sqrt{6}}{2};0\)]; (0;\(\frac{\sqrt{6}}{2}\)]; (\(\frac{\sqrt{6}}{2};+\infty\)], ta có:
\(y=-2x^3+3x\ge0\Leftrightarrow\left[{}\begin{matrix}x\le\frac{-\sqrt{6}}{2}\\0\le x\le\frac{\sqrt{6}}{2}\end{matrix}\right.\)
\(y=-2x^3+3x< 0\Leftrightarrow\left[{}\begin{matrix}x>\frac{\sqrt{6}}{2}\\0>x>\frac{-\sqrt{6}}{2}\end{matrix}\right.\)
Vậy hàm số lẻ.
Ttự với b,c,d.
a) Đặt y = f(x) = -2x3 + 3x. Tập xác định D = R
\(\forall x\in D\Rightarrow x\in R\Rightarrow-x\in R\Rightarrow-x\in R\)
\(f\left(-x\right)=-2\left(-x\right)^3+3\left(-x\right)=2x^3-3x=-f\left(x\right)\)
Vậy y = -2x3 + 3x là hàm số lẻ
b) Đặt \(y=f\left(x\right)=|x+2|-|x-2|\)
Tập xác định D = R
\(\forall x\in D\Rightarrow x\in R\Rightarrow-x\in R\Rightarrow-x\in R\)
\(f\left(-x\right)=|-x+2|-|-x-2|=|-\left(x-2\right)|-|-\left(x+2\right)|\)
\(=|x-2|-|x+2=-f\left(x\right)\)