
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(f\left( x \right) = \sqrt {x - 1} + \sqrt {2 - x} \)
Với mọi \({x_0} \in \left( {1;2} \right)\), ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {\sqrt {x - 1} + \sqrt {2 - x} } \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {x - 1} + \mathop {\lim }\limits_{x \to {x_0}} \sqrt {2 - x} \\ & \,\,\,\,\, = \sqrt {\mathop {\lim }\limits_{x \to {x_0}} x - \mathop {\lim }\limits_{x \to {x_0}} 1} + \sqrt {\mathop {\lim }\limits_{x \to {x_0}} 2 - \mathop {\lim }\limits_{x \to {x_0}} x} = \sqrt {{x_0} - 1} + \sqrt {2 - {x_0}} = f\left( {{x_0}} \right)\end{array}\)
Vậy hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( {1;2} \right)\).
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\sqrt {x - 1} + \sqrt {2 - x} } \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\sqrt {x - 1} + \sqrt {2 - x} } \right)\\ & = \sqrt {\mathop {\lim }\limits_{x \to {1^ + }} x - \mathop {\lim }\limits_{x \to {1^ + }} 1} + \sqrt {\mathop {\lim }\limits_{x \to {1^ + }} 2 - \mathop {\lim }\limits_{x \to {1^ + }} x} = \sqrt {1 - 1} + \sqrt {2 - 1} = 1 = f\left( 1 \right)\end{array}\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\sqrt {x - 1} + \sqrt {2 - x} } \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\sqrt {x - 1} + \sqrt {2 - x} } \right)\\ & = \sqrt {\mathop {\lim }\limits_{x \to {2^ - }} x - \mathop {\lim }\limits_{x \to {2^ - }} 1} + \sqrt {\mathop {\lim }\limits_{x \to {2^ - }} 2 - \mathop {\lim }\limits_{x \to {2^ - }} x} = \sqrt {2 - 1} + \sqrt {2 - 2} = 1 = f\left( 2 \right)\end{array}\)
Vậy hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {1;2} \right]\).

a) TXĐ: \(D = \mathbb{R}\)
Hàm số \(y = \sqrt {{x^2} + 1} \) xác định trên \(\mathbb{R}\) nên liên tục trên \(\mathbb{R}\).
Hàm số \(y = 3 - x\) là đa thức nên liên tục trên \(\mathbb{R}\).
Vậy hàm số \(y = \sqrt {{x^2} + 1} + 3 - x\) cũng liên tục trên \(\mathbb{R}\).
b) TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Hàm số \(y = \frac{{{x^2} - 1}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Hàm số \(y = \cos x\) là hàm lượng giác nên liên tục trên \(\mathbb{R}\). Vậy hàm số \(y = \cos x\) cũng liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Vậy hàm số \(y = \frac{{{x^2} - 1}}{x}.\cos x\) liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).

1.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)
2.
a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)
\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)
2b.
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)
- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)
- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)

Hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\).
Trên khoảng \(\left( {0; + \infty } \right)\), hàm số \(f\left( x \right)\) là hàm căn thức xác định trên \(\left( {0; + \infty } \right)\) nên hàm số liên tục trên khoảng \(\left( {0; + \infty } \right)\).
Trên khoảng \(\left( { - \infty ;0} \right)\), hàm số \(f\left( x \right)\) là hàm lượng giác xác định trên \(\left( { - \infty ;0} \right)\) nên hàm số liên tục trên khoảng \(\left( { - \infty ;0} \right)\).
Vậy hàm số \(f\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Ta có: \(f\left( 0 \right) = \sqrt {0 + 4} = 2\)
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \sqrt {x + 4} = \sqrt {0 + 4} = 2\)
\(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} 2\cos x = 2\cos 0 = 2\)
Vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = 2\) nên \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 2 = f\left( 0 \right)\).
Vậy hàm số liên tục tại điểm \(x = 0\).
Vậy hàm số liên tục trên \(\mathbb{R}\).

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{2-\sqrt{2x^2-4}}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{4-2x^2+4}{2+\sqrt{2x^2-4}}\cdot\dfrac{1}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{-2\left(x^2-4\right)}{-\left(x-2\right)\left(2+\sqrt{2x^2-4}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(2+\sqrt{2x^2-4}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2\left(x+2\right)}{2+\sqrt{2x^2-4}}=\dfrac{2\left(2+2\right)}{2+\sqrt{2\cdot2^2-4}}\)
\(=\dfrac{2\cdot4}{2+2}=\dfrac{8}{4}=2\)
\(f\left(2\right)=1\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)< >f\left(2\right)\)
=>Hàm số bị gián đoạn tại x=2

a) ĐKXĐ: \({x^2} - 4 \ne 0 \Leftrightarrow x \ne \pm 2\)
Vậy hàm số có TXĐ: \(D = \mathbb{R}\backslash \left\{ { \pm 2} \right\}\).
Hàm số \(f\left( x \right) = \frac{x}{{{x^2} - 4}}\) là hàm phân thức hữu tỉ nên nó liên tục trên các khoảng \(\left( { - \infty ; - 2} \right),\left( { - 2;2} \right)\) và \(\left( {2; + \infty } \right)\).
b) ĐKXĐ: \(9 - {x^2} \ge 0 \Leftrightarrow - 3 \le x \le 3\)
Vậy hàm số có TXĐ: \(D = \left[ { - 3;3} \right]\).
Hàm số \(g\left( x \right) = \sqrt {9 - {x^2}} \) là hàm căn thức nên nó liên tục trên khoảng \(\left( { - 3;3} \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \sqrt {9 - {x^2}} = \sqrt {9 - {3^2}} = 0 = f\left( 3 \right)\)
\(\mathop {\lim }\limits_{x \to - {3^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {3^ + }} \sqrt {9 - {x^2}} = \sqrt {9 - {{\left( { - 3} \right)}^2}} = 0 = f\left( { - 3} \right)\)
Vậy hàm số \(g\left( x \right) = \sqrt {9 - {x^2}} \) là liên tục trên đoạn \(\left[ { - 3;3} \right]\).
c) ĐKXĐ: \(\sin x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\)
Vậy hàm số có TXĐ: \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Hàm số \(h\left( x \right) = \cos x + \tan x\) là hàm lượng giác nên nó liên tục trên các khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right),k \in \mathbb{Z}\).

\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}-2x^2-4x=-2\cdot3^2-4\cdot3=-18-12=-30\)
\(f\left(3\right)=-2\cdot3^2-4\cdot3=-30\)
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=f\left(3\right)\)
=>f(x) liên tục tại x=3
Lời giải:
$\lim\limits_{x\to 3}f(x)=\lim\limits_{x\to 3}(-2x^2-4x)=-30=f(3)$ nên hàm liên tục tại $x=3$>

a) Ta có: g(2) = 5.
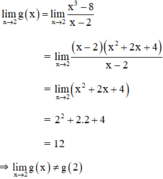
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
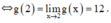
Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.
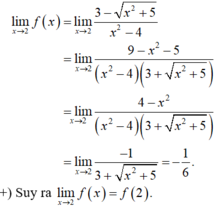
ĐKXĐ: \({x^2} - 4 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le - 2\end{array} \right.\)
Vậy hàm số có TXĐ: \(D = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\).
Hàm số \(y = \sqrt {{x^2} - 4} \) là hàm số căn thức nên nó liên tục trên các nửa khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \sqrt {{x^2} - 4} = \sqrt {{2^2} - 4} = 0 = f\left( 2 \right)\)
\(\mathop {\lim }\limits_{x \to - {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {2^ + }} \sqrt {{x^2} - 4} = \sqrt {{{\left( { - 2} \right)}^2} - 4} = 0 = f\left( { - 2} \right)\)
Vậy hàm số \(y = \sqrt {{x^2} - 4} \) liên tục trên các nửa khoảng \(\left( { - \infty ; - 2} \right]\) và \(\left[ {2; + \infty } \right)\).