GPT; \(x^3+\sqrt{\left(1-x^2\right)^3}=x\sqrt{2\left(1-x^2\right)}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
11 tháng 4 2016
Bạn tự phân tích đa thức thành nhân tử nhé!
\(1.\)
\(2x^3+x+3=0\)
\(\Leftrightarrow\) \(\left(x+1\right)\left(2x^2-2x+3\right)=0\) \(\left(1\right)\)
Vì \(2x^2-2x+3=2\left(x^2-x+1\right)+1=2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}>0\) với mọi \(x\in R\)
nên từ \(\left(1\right)\) \(\Rightarrow\) \(x+1=0\) \(\Leftrightarrow\) \(x=-1\)
TN
1
21 tháng 8 2020
\(2\left(x^2+2\right)=5\sqrt{x^3+1}\left(đk:x\ge-1\right)\)
\(\Leftrightarrow2\left[\left(x^2-x+1\right)+\left(x+1\right)\right]=5\sqrt{\left(x+1\right)\left(x^2-x+1\right)}\)
Đặt \(\hept{\begin{cases}\sqrt{x^2+1}=a\left(a\ge0\right)\\\sqrt{x^2-x+1}=b\left(b>0\right)\end{cases}}\)
Tìm được \(\orbr{\begin{cases}a=2b\\b=2a\end{cases}}\)
TH1: a=2b => phương trình vô nghiệm
TH2: b=2a ta được \(x_1=\frac{5+\sqrt{37}}{2};x_2=\frac{5-\sqrt{37}}{2}\left(tmđk\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 12 2021
\(cotx=cot70^0\)
\(\Rightarrow x=70^0+k180^0\) (\(k\in Z\))
H
8 tháng 4 2023
`|x - 6| = -5x + 9`
\(\Leftrightarrow\left[{}\begin{matrix}x-6=-5x+9\\x-6=5x-9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5x=9+6\\x-5x=-9+6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}6x=15\\-4x=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15}{6}=\dfrac{5}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2020
\(\Leftrightarrow2cos\frac{3x}{2}.cos\frac{x}{2}=2sin\frac{3x}{2}.cos\frac{3x}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\frac{3x}{2}=0\\cos\frac{x}{2}=sin\frac{3x}{2}=cos\left(\frac{\pi}{2}-3x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{3x}{2}=\frac{\pi}{2}+k\pi\\\frac{x}{2}=\frac{\pi}{2}-3x+k2\pi\\\frac{x}{2}=3x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+\frac{k2\pi}{3}\\x=\frac{\pi}{7}+\frac{k4\pi}{7}\\x=\frac{\pi}{5}+\frac{k4\pi}{5}\end{matrix}\right.\)
ID
10 tháng 5 2022
\(\Leftrightarrow2\sin2x=\sqrt{2}\)
\(\Leftrightarrow\sin2x=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sin2x=\dfrac{\pi}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{4}+k2\pi\\2x=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+k\pi\\x=\dfrac{3\pi}{8}+k\pi\end{matrix}\right.\left(k\in Z\right)\)
ID
10 tháng 5 2022
\(\sin x=\dfrac{1}{2}\Leftrightarrow\sin x=\sin\dfrac{\pi}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\pi-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\left(k\in Z\right)\)
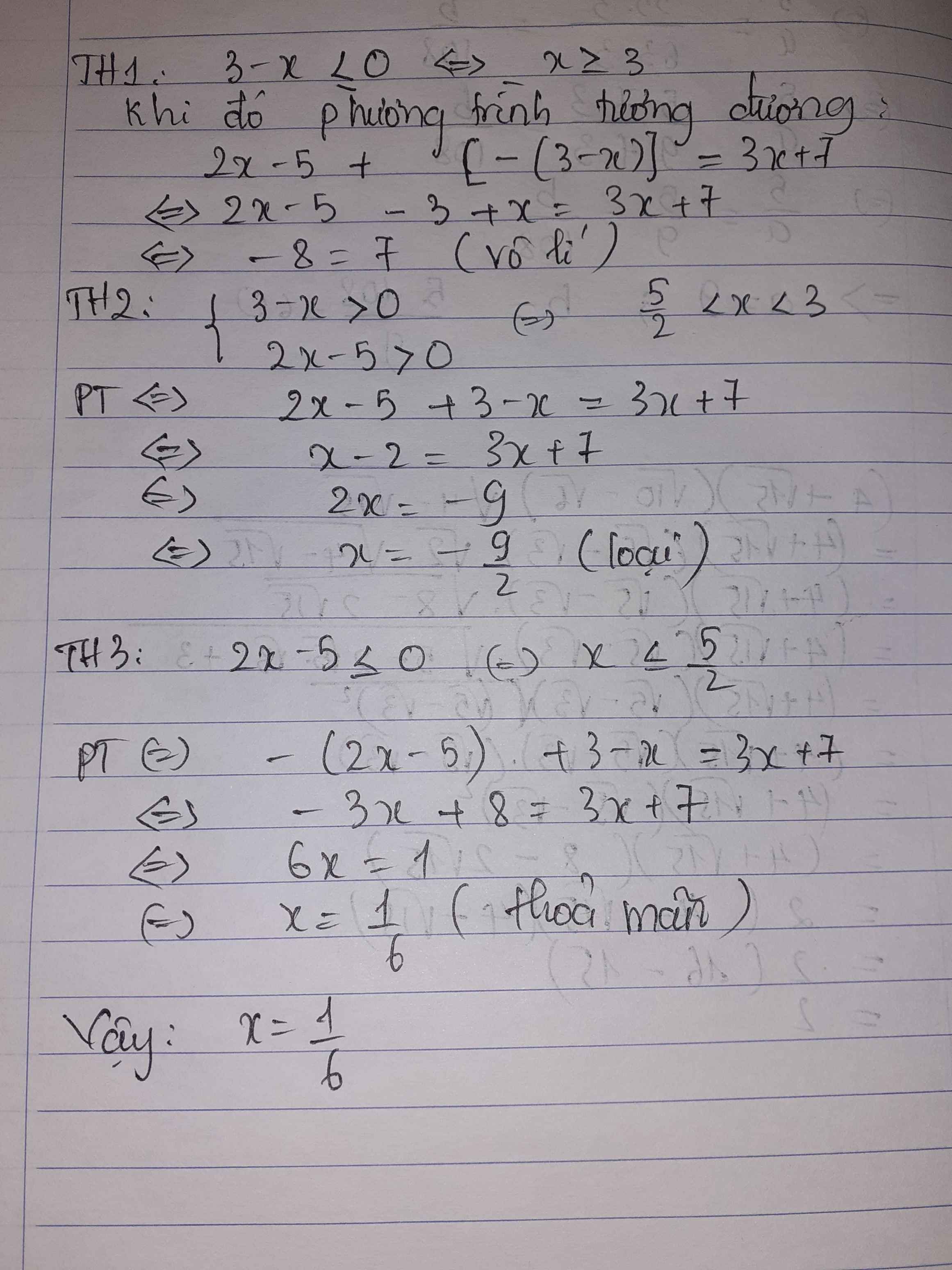
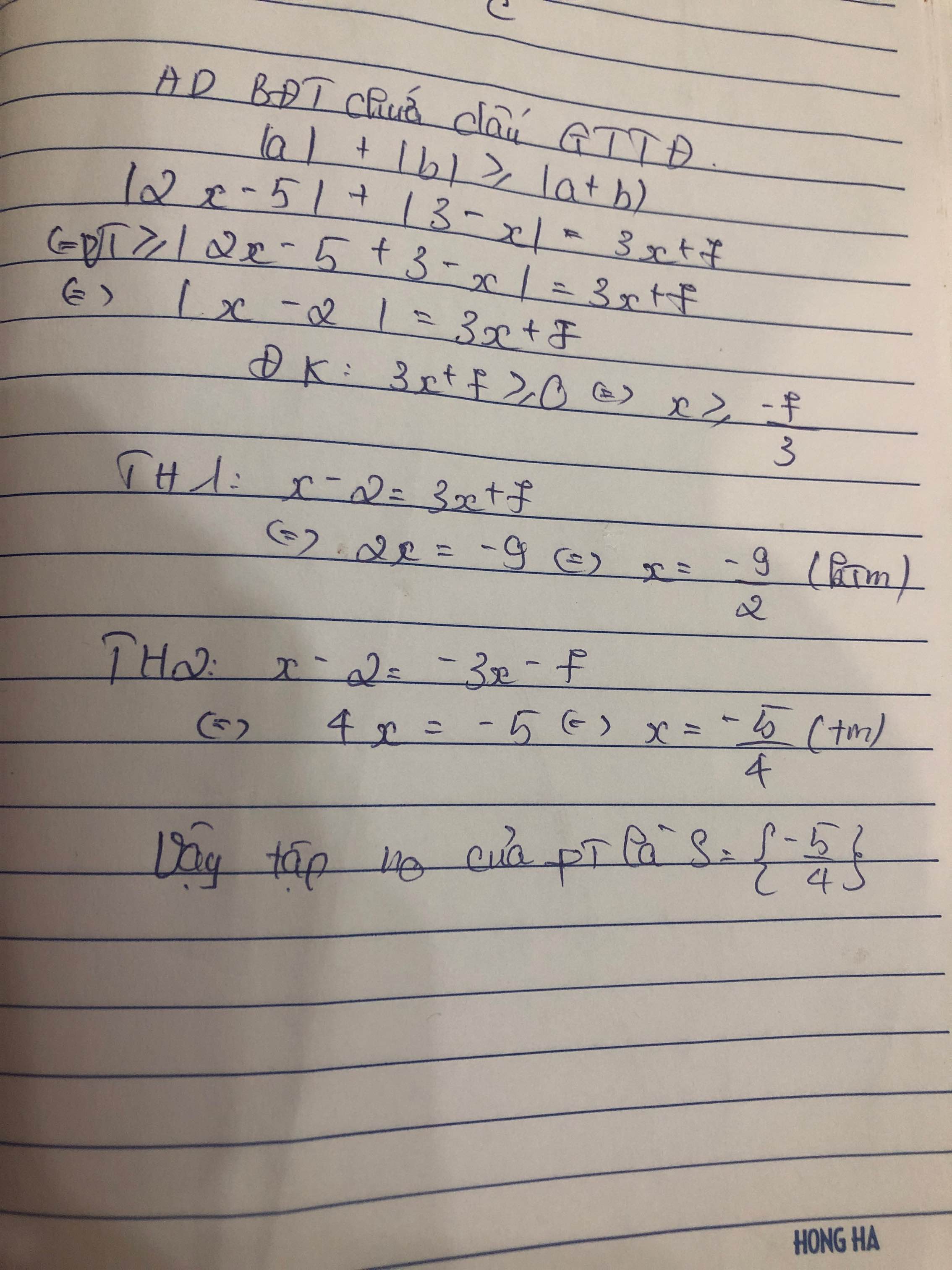
ĐK: \(-1\le x\le1\)
Đặt \(\sqrt{1-x^2}=y\)\(\Rightarrow y^2+x^2=1\Leftrightarrow\left(x+y\right)^2-2xy=1\)
Pt đã cho thành: \(x^3+y^3=xy\sqrt{2}\Leftrightarrow\left(x+y\right)^3-3xy\left(x+y\right)-xy\sqrt{2}=0\)
Đặt \(x+y=a;\text{ }xy=b\)
Ta có: \(a^2-2b=1;\text{ }a^3-3ab-b\sqrt{2}=0\)
\(a^2-2b=1\Rightarrow b=\frac{a^2-1}{2}\)
\(a^3-3ab-b\sqrt{2}=0\Leftrightarrow a^3-3a.\frac{a^2-1}{2}-\frac{a^2-1}{2}\sqrt{2}=0\)
\(\Leftrightarrow-a^3-\sqrt{2}a^2+3a+\sqrt{2}=0\)
\(\Leftrightarrow\left(a-\sqrt{2}\right)\left(a+\sqrt{2}-1\right)\left(a+\sqrt{2}+1\right)=0\)
\(\Leftrightarrow a=\sqrt{2}\text{ hoặc }a=1-\sqrt{2}\text{ hoặc }a=-1-\sqrt{2}\)
\(+a=\sqrt{2};\text{ }b=\frac{2-1}{2}=\frac{1}{2}\)\(\Rightarrow x+y=\sqrt{2};\text{ }xy=\frac{1}{2}\)
=> x,y là 2 nghiệm của pt \(X^2-\sqrt{2}X+\frac{1}{2}=0\Leftrightarrow\left(X-\frac{1}{\sqrt{2}}\right)^2=0\Leftrightarrow X=\frac{1}{\sqrt{2}}\)
\(\Rightarrow x=\sqrt{1-x^2}=\frac{1}{\sqrt{2}}\text{ (nhận)}\)
\(+a=1-\sqrt{2}\Rightarrow b=1-\sqrt{2}\Rightarrow x+y=xy=1-\sqrt{2}\)
=> x, y là 2 nghiệm của pt \(X^2-\left(1-\sqrt{2}\right)X+1-\sqrt{2}=0\)
\(\Leftrightarrow X=\frac{1-\sqrt{2}+\sqrt{2\sqrt{2}-1}}{2}>0\text{ hoặc }X=\frac{1-\sqrt{2}-\sqrt{2\sqrt{2}-1}}{2}