\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(t^2+6yt+9y^2\right)+\left(4y^2-12y+9\right)=0\)

\(\Leftrightarrow\left(x+y\right)^2+\left(t+3y\right)^2+\left(2y-3\right)^2=0\)

Dấu '=' xảy ra khi y=3/2; x=-3/2; t=-3y=-9/2

\(x^2+2xy+y^2+9y^2+6yt+t^2+4y^2-12y+9=0\)

\(\Leftrightarrow\left(x+y\right)^2+\left(3y+t\right)^2+\left(2y-3\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+y=0\\3y+t=0\\2y-3=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=\frac{3}{2}\\t=\frac{-9}{2}\\x=\frac{-3}{2}\end{matrix}\right.\)

pt <=> (x² + 2xy + y²) + (t² + 6yt + 9y²) + (4y² - 12y + 9) = 0

<=> (x + y)² + (t + 3y)² + (2y - 3)² = 0

<=> \(\left\{{}\begin{matrix}\left(x+y\right)^2=0\\\left(t+3y\right)^2=0\\\left(2y-3\right)^2=0\end{matrix}\right.\)

<=> \(\left\{{}\begin{matrix}x=-y=-\dfrac{3}{2}\\t=-3y=-\dfrac{9}{2}\\y=\dfrac{3}{2}\end{matrix}\right.\)

Vậy ...

\(a,\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{7}{4}=0\\ \Leftrightarrow\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}=0\\ \Leftrightarrow x,y\in\varnothing\left[\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\right]\\ b,\Leftrightarrow\left(x^2-2x+1\right)+\left(9y^2+12y+4\right)+\left(4z^2-4z+1\right)+14=0\\ \Leftrightarrow\left(x-1\right)^2+\left(3y+2\right)^2+\left(2z-1\right)^2+14=0\\ \Leftrightarrow x,y,z\in\varnothing\left[\left(x-1\right)^2+\left(3y+2\right)^2+\left(2z-1\right)^2+14\ge14>0\right]\)

\(c,\Leftrightarrow-\left(x^2-10xy+25y^2\right)-\left(y^2-20y+100\right)-50=0\\ \Leftrightarrow-\left(x-5y\right)^2-\left(y-10\right)^2-50=0\\ \Leftrightarrow x,y\in\varnothing\left[-\left(x-5y\right)^2-\left(y-10\right)^2-50\le-50< 0\right]\)

\(x^2+2y+2xy+10x+12y+26=0\)

\(\Leftrightarrow\left[\left(x^2+2xy+y^2\right)+\left(10x+10y\right)+25\right]+\left(y^2+2y+1\right)=0\)

\(\Leftrightarrow\left[\left(x+y\right)^2+10\left(x+y\right)+25\right]+\left(y+1\right)^2=0\)

\(\Leftrightarrow\left(x+y+5\right)^2+\left(y+1\right)^2=0\)

Vì \(\left(x+y+5\right)^2+\left(y+1\right)^2\ge0\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y+5=0\\y+1=0\end{cases}\Rightarrow\hept{\begin{cases}x=-4\\y=-1\end{cases}}}\)

Vậy \(x=-4;y=-1\)

<=> [ (x^2+2xy+y^2)+ 2.(x+y).5 +25 ] + (y^2+2y+1)=0

<=> (x+y+5)^2 + (y+1)^2 = 0

<=> x+y+5 = 0 và y+1 = 0

<=> x=-4 và y=-1

Ta có: x²+2y²+2xy+10x+12y+26=0

=> (x²+2xy+y²)+(10x+10y)+25+(y²+2y+1)=0

=> (x+y)²+10(x+y)+25+(y²+2y+1)=0

=> (x+y+5)²+(y+1)²=0

=> (x+y+5)²=(y+1)²=0

=> x+y+5=y+1=0

(+) y+1=0=> y=-1

(+) x+y+5=0 mà y=-1=> x-1+5=0

=> x+4=0=> x=-4

Vậy (x,y)=(-4;-1)

1. ( 3x + 2)² - 4

= (3x+2-2)(3x+2+2)

= 3x(3x+4)

2. 4x² - 25y²

= (2x-5y)(2x+5y)

3. 4x²- 49

=(2x-7)(2x+7)

4. 8z³ + 27

=(2z+3)(4x²-6z+9)

5. \(\dfrac{9}{25}x^4-\dfrac{1}{4}\)

= \((\dfrac{3}{5}x^2-\dfrac{1}{2})(\dfrac{3}{5}x^2+\dfrac{1}{2})\)

6. x³²  - 1

=(x¹⁶-1)(x¹⁶+1)

7. 4x² + 4x + 1

=(2x+1)²

8. x² - 20x + 100

=(x-10)²

9. y⁴ -14y² + 49

=(y²-7)²

10.  125x³ - 64y³

= (5x-4y)(25x²+20xy+16y²)

1) \(\left(3x+2\right)^2-4=\left(3x+2+2\right)\left(3x+2-2\right)=3x\left(3x+4\right)\)

2) \(4x^2-25y^2=\left(2x-5y\right)\left(2x+5y\right)\)

3) \(4x^2-49=\left(2x-7\right)\left(2x+7\right)\)

4) \(8z^3+27=\left(2z+3\right)\left(4z^2-6z+9\right)\)

5) \(\dfrac{9}{25}x^4-\dfrac{1}{4}=\left(\dfrac{3}{5}x^2-\dfrac{1}{2}\right)\left(\dfrac{3}{5}x^2+\dfrac{1}{2}\right)\)

6) \(x^{32}-1=\left(x^{16}-1\right)\left(x^{16}+1\right)\)

\(=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)

\(=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)

7) \(4x^2+4x+1=\left(2x+1\right)^2\)

8) \(x^2-20x+100=\left(x-10\right)^2\)

9) \(y^4-14y^2+49=\left(y^2-7\right)^2\)

Điều kiện x ≥ − 7 y ≥ − 1 3 *

x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9             ( 1 ) x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0       ( 2 )

Có 1 ⇔ x 2 + 2 y + 4 x − 3 y 2 − 12 y − 9   = 0 , ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được x = − 3 y − 9 x = y + 1

Với x = − 3 y − 9 thì (*) ⇒ − 3 y − 9 ≥ − 7 y ≥ − 1 3 ⇔ y ≤ − 2 3 y ≥ − 1 3 (vô lí)

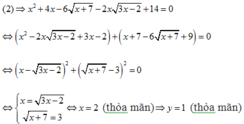
Hệ phương trình có nghiệm là 2 ; 1 ⇒ a = 2 , b = 1 ⇒ T = 24

Đáp án cần chọn là: A

6xy+4x-3y=8
=> 6xy -3y=8-4x
=>3y(2x-1)= -2(2x-1) +6
=>(2x-1)(3y+2)=6
mà x,y thuộc Z =>(2x-1),(3y+2)  thuộc Z =>(2x-1),(3y+2) thuộc U(6)   xong giải ra bình thường nhé mấy câu sau tương tự 
 

chị giải nốt cho em phần a với ạ