Tại sao khi giải pt asin²x +bsinxcosx +c.cos²x=d thì lại đặt cosx bằng 0 nữa vậy ạ. Mình chỉ đặt cos x khác 0 là được mà.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn học đạo hàm rồi chớ, gia tốc chính là đạo hàm của vận tốc. Bạn đem phương trình vận tốc đi đạo hàm theo t thì sẽ được phương trình a=20pi.4pi.cos(4pi.t)=80pi^2.cos(4pi.t)=80.10.cos(4pi.t)=800cos(4pi.t)
Sau đó, thay t = 0 vào phương trình gia tốc, ta được: a = 800(cm/s)= 8(m/s)
Chọn A. Bạn cứ liên hệ nếu không rõ nhé!

Pt xác định khi:
\(\left\{{}\begin{matrix}5x-4\ge0\\2-x\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{4}{5}\\x\le2\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{4}{5}\le x\le2\)
Nhưng trong TH này cậu phải làm cả hai nhé !
\(\sqrt[]{5x-4}=2-x\)
Phải lấy điều kiện \(2-x\ge0\) vì phương trình trên có dạng :
\(\sqrt[]{A}=B\) nên khi đặt điều kiện \(B\ge0\) thì chắc chắn \(\sqrt[]{A}\ge0\)
Nên không cần điều kiện \(A\ge0\) mà chỉ cần điều kiện \(B\ge0\) hay \(2-x\ge0\) là đủ.

Nếu mẫu là \(\left(x+3\right)\left(x-3\right)\) thì điều kiện xác định sẽ là:
\(\left\{{}\begin{matrix}x+3\ne0\\x-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-3\\x\ne3\end{matrix}\right.\)
- Lưu ý là cả \(x+3\) và \(x-3\) đều phải khác 0

Bởi vì ta có tính chất:
`a>=b>0=>1/a<=1/b`
GTLN bởi vì có dấu `<=`

Nếu em thay $x=9,10,...$ không ra kết quả thì có nghĩa bài toán không có nghiệm $x=9,10,...$ thôi.
Em xét 3 TH:
$x\geq 7$
$3\leq x< 7$
$x< 3$
Để phá trị tuyệt đối
Còn không có chuyện phải thay $x\leq 7$

\(\Leftrightarrow2-6sinx.cosx-2sinx+2cosx+2cos^2x=0\)
\(\Leftrightarrow3\left(1-2sinx.cosx\right)-2\left(sinx-cosx\right)+cos^2x-sin^2x=0\)
\(\Leftrightarrow3\left(sinx-cosx\right)^2-2\left(sinx-cosx\right)-\left(sinx-cosx\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\Leftrightarrow x=\frac{\pi}{4}+k\pi\\sinx-2cosx=1\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow\frac{1}{\sqrt{5}}sinx-\frac{2}{\sqrt{5}}cosx=\frac{1}{\sqrt{5}}\)
Đặt \(\frac{1}{\sqrt{5}}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow sinx.cosa-cosx.sina=cosa\)
\(\Leftrightarrow sin\left(x-a\right)=sin\left(\frac{\pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-a=\frac{\pi}{2}-a+k2\pi\\x-a=a+\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=2a+\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

cái này thì ko nhất thiết phải Cm nha bạn
Câu b kêu tìm x để B ko nhỏ hơn hoặc bằng A
Nghĩa là
\(\dfrac{4}{3-\sqrt{x}}>1\)
\(\Leftrightarrow\dfrac{4}{3-\sqrt{x}}-1>0\)
\(\Leftrightarrow\dfrac{4-\left(3-\sqrt{x}\right)}{3-\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{3-\sqrt{x}}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}+1>0\\3-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}+1< 0\left(VL\right)\\3-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Theo Đk ta có x≥0
Vậy 0≤x<9 thì B ko nhỏ hơn hoặc bằng A
\(\sqrt{x}\ge0\Leftrightarrow\sqrt{x}+1\ge1>0\)
Hiển nhiên nhé

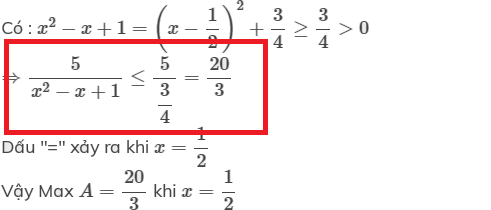


Như vậy sẽ có rất nhiều trường hợp thiếu nghiệm, đó là khi \(a=d\) (mất 1/2 số điểm đó em)
Ví dụ: giải phương trình
\(2sin^2x+3sinx.cosx+cos^2x=2\)
Trường hợp này ko xét \(cosx=0\) là mất nửa số điểm rồi (mất hẳn 1 họ nghiệm)