Cho tam giác ABC có góc A= góc B + C . Hai đường phân giác của góc A và
góc C cắt nhau tại O. Tại sao khi đó số đo BOC bằng bao nhiêu vậy
Mai mik thi rồi giúp mik với
Thank
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 1 2022
Xét ΔABC có \(\widehat{A}=\widehat{B}+\widehat{C}\)
nên ΔABC vuông tại A
Xét ΔABC có
AO là phân giác
CO là phân giác
Do đó: BO là phân giác của góc CBA
\(\widehat{OCB}+\widehat{OBC}=\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ABC}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
nên \(\widehat{BOC}=135^0\)
CM
20 tháng 1 2017
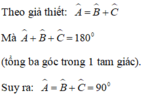
Do AO, CO lần lượt là tia phân giác của ∠A và ∠C nên BO là tia phân giác của ∠B
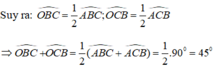
Xét tam giác OBC có:
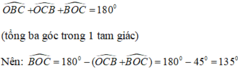
Chọn (C) 135º.
11 tháng 4 2023
a: góc A=180/2=90 độ
b: góc OBC+góc OCB=90/2=45 độ
=>góc BOC=135 độ
Mình có cách này bạn xem thử và check nhé!
Do tam giác ABC có \(\widehat{A}=\widehat{B}+\widehat{C}\). Mà tổng ba góc trong tam giác là 180o nên \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Leftrightarrow\widehat{A}+\widehat{A}=180^o\Leftrightarrow2.\widehat{A}=180^o\Leftrightarrow\widehat{A}=90^o=\widehat{B}+\widehat{C}\). Do đó tam giác ABC vuông tại A.
Ta có: Xét tam giác ABC,theo định lí về tổng số đo của ba góc trong tam giác,ta suy ra
\(\widehat{BOC}=180^o-\left(\widehat{B_1}+\widehat{C_1}\right)\) (1)
\(=180^o-\left(\widehat{B}+\widehat{C}-\widehat{B_2}-\widehat{C_2}\right)=180^o-90^o+\widehat{B_2}+\widehat{C_2}=90^o+\widehat{B_2}+\widehat{C_2}=90^o+\widehat{B_1}+\widehat{C_1}\) (2) (do \(\widehat{B_1}=\widehat{B_2};\widehat{C_1}=\widehat{C_2}\)).Từ (1) và (2),ta có: \(180^o-\left(\widehat{B_1}+\widehat{C_1}\right)=90^o+\widehat{B_1}+\widehat{C_1}\Rightarrow180^o-90^o=2\left(\widehat{B_1}+\widehat{C_1}\right)\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=45^o\). Thay vào (1) (hoặc thay vào (2) cũng được) ,ta suy ra: \(\widehat{BOC}=180^o-\left(\widehat{B_1}+\widehat{C_1}\right)=180^o-45=135^o\)