Trong mặt phẳng cho hai đường thẳng a//b.Chứng minh mọi đường thẳng cắt a thì phải cắt b ( chứng minh phản chứng)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
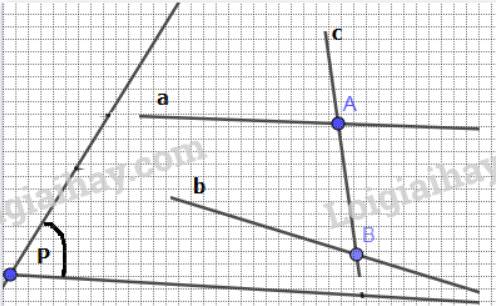
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B
Ta có A thuộc a mà a nằm trong mp(P) suy ra A cũng nằm trong mp(P)
B thuộc b mà b nằm trong mp(P) suy ra B cũng nằm trong mp(P)
Suy ra đường thẳng AB cũng nằm trong mp(P) tức c cũng nằm trong mp(P).

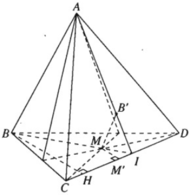
a) MB' qua M và song song với (ABC) và (ABD) ⇒ MB′ song song với giao tuyến AB của hai mặt phẳng này. Ta có: MB′ // AB nên MB' và AB xác định một mặt phẳng. Giả sử MB cắt AB' tại I.
Ta có: I ∈ BM ⇒ I ∈ (BCD)
I ∈ AB′ ⇒ I ∈ (ACD)
Nên I ∈ (BCD) ∩ (ACD) = CD
Có: I ∈ CD
Vậy ba đường thẳng AB', BM và CD đồng quy tại I.
b) MB′ // AB 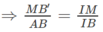
Kẻ MM′ ⊥ CD và BH ⊥ CD
Ta có: MM′ // BH 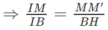
Mặt khác:
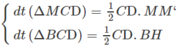
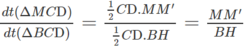
Do đó: 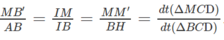
Vậy 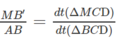
c) Tương tự ta có: 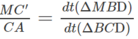
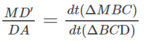
Vậy:
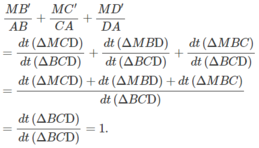

Ta có (P) // (Q)
Suy ra AA’ // BB’ (1)
Ta có a // b
Suy ra AB // A’B’ (2)
Từ (1) và (2) suy ra AA’B’B là hình bình hành
Do đó AB = A’B’

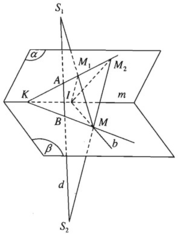
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.

Đáp án D
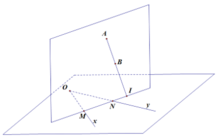
AB và mặt phẳng (Ox, Oy) luôn có điểm chung I
α chứa AB
⇒ I luôn nằm trên giao tuyến của α và (Ox, Oy) (1)
Ta lại có: α thay đổi cắt Ox tại M, Oy tại N
Xét α và (Ox, Oy) có M và N là điểm chung
⇒ MN là giao tuyến của 2 mặt phẳng (2)
(1);(2): M, N, I thẳng hàng
⇒ MN luôn đi qua I cố định
Giả sử m là đường thẳng song song với b và cắt qua a. Vì m song song với b mà b song song với a nên m cũng song song với a ( vô lí ) Vậy m không song song với b tức m cắt b