Giải giúp em bài 1 đc kg ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: \(\dfrac{2-\sqrt{3}}{3\sqrt{6}}=\dfrac{2\sqrt{6}-3\sqrt{2}}{18}\)
b: \(\dfrac{1}{\sqrt{3}+\sqrt{2}}=\sqrt{3}-\sqrt{2}\)

Bài 1:
a: \(-xy\sqrt{\dfrac{y}{x}}=-xy\cdot\dfrac{\sqrt{xy}}{x}=-y\sqrt{xy}\)
b: \(\sqrt{\dfrac{-3x^2}{35}}=\dfrac{\sqrt{105}x}{35}\)


Bài 3:
\(a,=\dfrac{53\left(9+2\sqrt{7}\right)}{53}+2\sqrt{7}-5=9+2\sqrt{7}+2\sqrt{7}-5=4+4\sqrt{7}\)
a: Sửa đề: \(\dfrac{53}{9-2\sqrt{7}}+2\sqrt{7}-5\)
\(=9+2\sqrt{7}+2\sqrt{7}-5\)
\(=4\sqrt{7}+4\)

bài 3:
b: \(\dfrac{2}{\sqrt{3}+1}+\dfrac{1}{2-\sqrt{3}}+\dfrac{6}{3+\sqrt{3}}\)
\(=\sqrt{3}-1+2+\sqrt{3}+\sqrt{3}-1\)
\(=3\sqrt{3}\)

Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$

Gọi số sách là x
Theo đề, ta có: \(x+2\in BC\left(10;25\right)\)
\(\Leftrightarrow x+2\in B\left(50\right)\)
mà x là số lớn nhất có 3 chữ số và thỏa mãn đề bài
nên x+2=1000
hay x=998


buổi chiều bán được là: (300- 125) x 3/5 = 105 (kg)
cả hai buổi bán được là: 180 + 105 = 285 (kg)
buổi chiều bán được là
(300- 125) x 3/5 = 105 (kg)
cả hai buổi bán được là:
180 + 105 = 285 (kg)


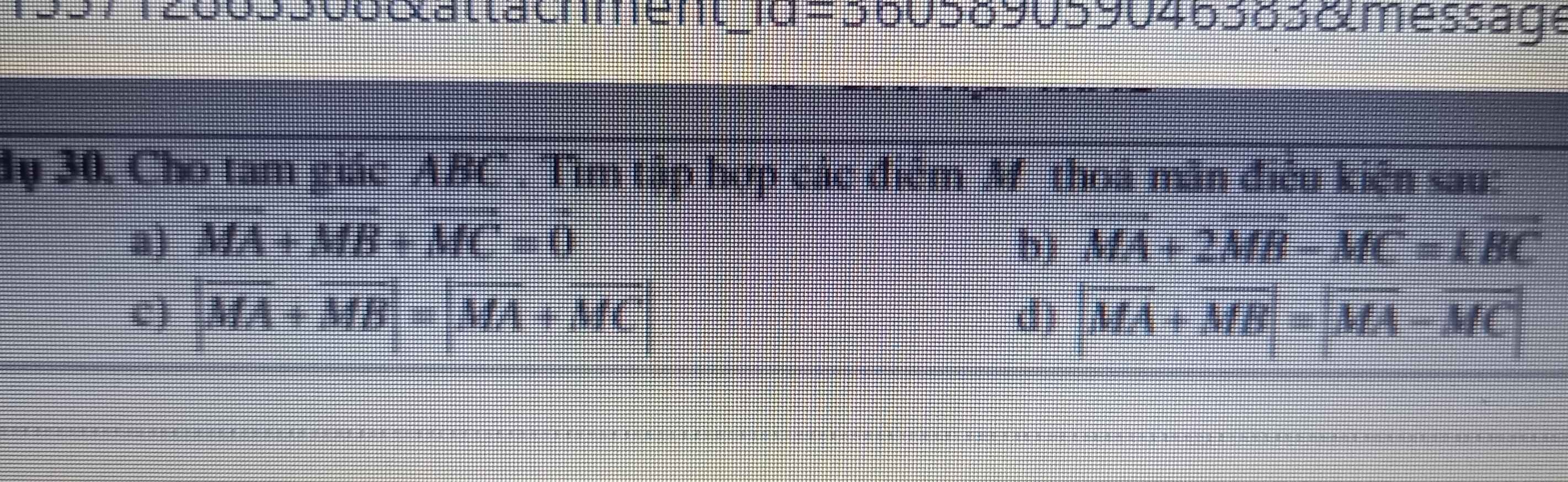


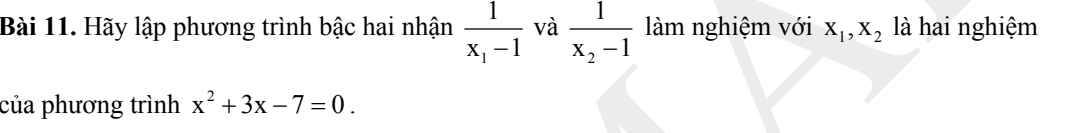

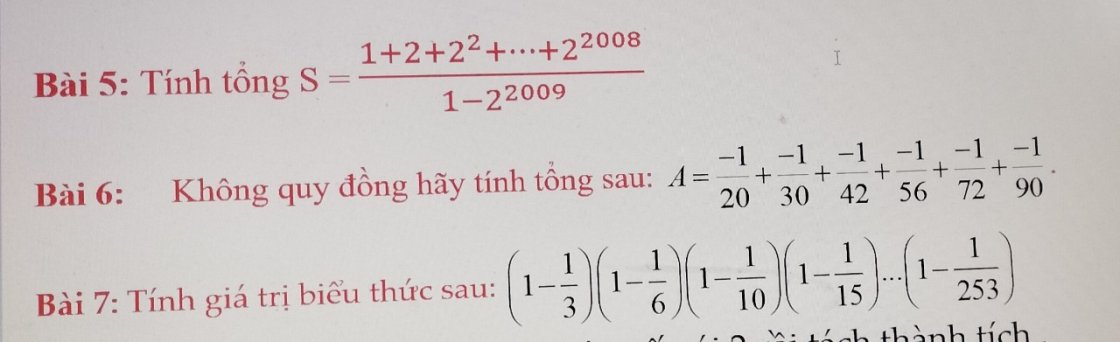 các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
a. \(R=U:I=30:3=10\Omega\)
b. \(I'=U':R=20:10=2A\)