Cho tam giác ABC: M, N, P là trung điểm của BC, CA, AB; O là giao điểm của 3 đường trung trực; các đường cao AD, BE, CF cắt nhau tại H; I, K, R là trung điểm của HA, HB, HC. Chứng minh rằng I, K, R, M, N, P, D, E, F cùng thuộc 1 đường trong ơ-le
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 4 2018
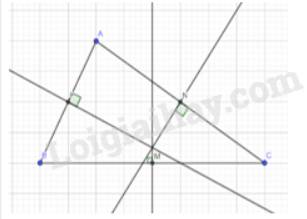
Giả sử MN: y = a x + b
Ta có N thuộc MN 0 = a . 1 + b ⇔ a = − b
M thuộc MN 1 = a . 0 + b ⇔ b = 2 ⇔ a = − 2 ⇒ b = 2
Do đó MN: y = − 2 x + 2
Vì M, N lần lượt là trung điểm của các cạnh BC, CA của tam giác ABC nên MN là đường trung bình của tam giác ABC MN // AB
Suy ra AB có dạng: y = − 2 x + b ’ ( b ’ ≠ 2 )
Vì P là trung điểm của AB nên AB đi qua P (−1; −1 )
⇔ − 1 = − 2 ( − 1 ) + b ’ ⇒ b ’ = − 3 ( t / m )
Vậy AB: y = − 2 x – 3
Đáp án cần chọn là: C
CM
23 tháng 1 2019
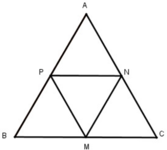
Ta có: M là trung điểm của BC
N là trung điểm của AC nên MN là đường trung bình của Δ ABC ⇒ MN = 1/2 AB
Ta có: P là trung điểm của AB nên MP là đường trung bình của △ ng bình của △ ABC ⇒ NP = 1/2 BC
Mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy △ MNP đều
Trong tam giác ABH có PK là đường trung bình nên PK//AH và \(PK=\frac{1}{2}AH\)
Trong tam giác ACH có NR là đường trung bình nên NR//AH và \(NR=\frac{1}{2}AH\)
Do đó PK//NR và PK=NR nên PNRK là hình bình hành
Mặt khác PK//AH mà AH _|_ BC => PK _|_ BC
Lại có PN //BC (do PN là đường trung bình tam giác ABC)
=> PN _|_ PK, do đó PNRK là hình chữ nhật
Gọi S là giao của PR và NK thì SP=SN=SK=SR
Chứng minh tương tự có IS=SM=SN=SK
Tam giác FPR vuông tại F có S là trung điểm PR nên SF=SP=SR
Tương tự cũng có SE=SK=SN; SD=SI=SM
=> SD=SE=SF=SM=SN=SP=SI=SK=SR
Vậy 9 điểm I,K,R,M,N,P,D,E,F cùng thuộc 1 đường tròn tâm I
Đường tròn đi qua 9 điểm được gọi là đường tròn Euler của tam giác ABC