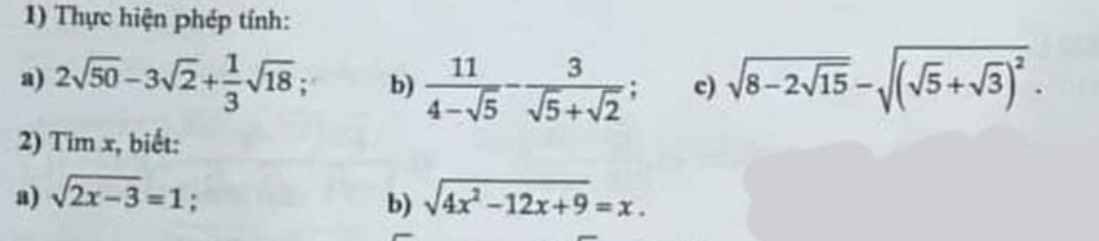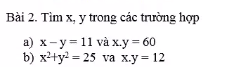Câu 1 : Nội dung của bài là 

+) Người cha muốn đứa con trở thành một người chính trực 

+) Cho chúng ta thấy được tình cảm của cha mẹ không bao giờ thay đổi cho dù con có trở thành bất kì ai

Câu 2

Lời dẫn trực tiếp trong bài là : kinh tamub ..... con trai ngươi "

 Chuyển :

+) Kinh Tamud nói rằng khi bạn dạy điều gì cho con trai bạn thì đó cung như việc ban dang dạy cho con trai của con trai bạn

Câu 3 

Ý nghĩa :

+ ) Ám chỉ trẻ con như chiếc gương phản chiếu của chúng ta , khi chúng ta dạy nó một điều nào đó , nó sẽ dạy cho đứa con của mình như vậy

Câu 4 

+) Người cha dã dạy cho con : tương lai của con là do con quyết định ,trở thành người xấu hay tốt cũng là do con nhưng người cha mong muốn đứa con của mình trở thành một người chính trực

Ý 2 mình chưa nghĩ ra mong bạn thông cảm 

Câu 5

Em cảm nhận bài học là 

+) cha mẹ luôn là người đối tốt với ta nhất 

+) Mong con trở thành một người tốt 

                                                  Mình không biết viết như thế nào nữa rồi 

                                                                     Xin lỗi bạn nha 

Lời giải:
Gọi vận tốc ban đầu là $x$ km/h 

Thời gian dự định: $\frac{AB}{x}$ (h) 

Khi vận tốc tăng $a$ km/h thì thời gian đi là: $\frac{AB}{x+a}$ (h) 

$\frac{AB}{x}-\frac{AB}{x+a}=0,5$ 

$\Leftrightarrow \frac{aAB}{x(x+a)}=0,5(*)$

Khi vận tốc giảm $b$ km/h thì thời gian đi là: $\frac{AB}{x-b}$ (h) 

$\frac{AB}{x-b}-\frac{AB}{x}=1$ 

$\Leftrightarrow \frac{bAB}{x(x-b)}=1(**)$

Từ $(*); (**)\Rightarrow \frac{x-b}{x+a}.\frac{a}{b}=0,5$

$\Leftrightarrow 2a(x-b)=b(x+a)$

$\Leftrightarrow 2ax-2ab=bx+ab$

$\Leftrightarrow x(2a-b)=3ab$
$\Rightarrow  x=\frac{3ab}{2a-b}$

Đến đây bạn thay $a,b$ vô để tính thôi.

e cảm ơn ạ

Gọi tọa độ của M là: \(M_{\left(x;y\right)}\)

Ta có: \(\left\{{}\begin{matrix}\overrightarrow{MA}_{\left(-2-x;4-y\right)}\\\overrightarrow{MB}_{\left(1-x;-y\right)}\\3\overrightarrow{MC}_{\left(9-3x;-6-3y\right)}\end{matrix}\right.\)

 \(\overrightarrow{MA}+\overrightarrow{MB}=3\overrightarrow{MC}\)

Ta lại có: \(\left(\overrightarrow{MA}+\overrightarrow{MB}\right)_{\left(-1-2x;4-2y\right)}\)

Suy ra: \(\left\{{}\begin{matrix}-1-2x=9-3x\\4-2y=-6-3y\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=-10\end{matrix}\right.\)

Vậy tọa độ điểm M là: \(M_{\left(10;-10\right)}\)

Cả 2 câu luôn ạ

Câu 1 :

a, Ta có : EF//BC

Theo định lý Ta-lét, ta có :

\(\Rightarrow\dfrac{AE}{EB}=\dfrac{AF}{FC}\)

hay \(\dfrac{4}{BE}=\dfrac{6}{3}\)

\(\Rightarrow BE=\dfrac{4.3}{6}=2\)

b, Ta có : DK là phân giác \(\widehat{EDF}\) ( hình hơi mờ và còn sai góc nữa bạn)

\(\Rightarrow\dfrac{EK}{KF}=\dfrac{ED}{DF}\)

hay \(\dfrac{EK}{KF}=\dfrac{12}{16}=\dfrac{3}{4}\)

\(\Rightarrow\dfrac{EK}{3}=\dfrac{KF}{4}=\dfrac{EK+KF}{3+4}=\dfrac{18}{7}\)

\(\Rightarrow EK=\dfrac{18}{7}.3=\dfrac{54}{7}\)

\(\Rightarrow KF=\dfrac{18}{7}.4=\dfrac{72}{7}\)

1)

a) \(2\sqrt{50}-3\sqrt{2}+\dfrac{1}{3}\sqrt{18}\)

\(=2\cdot5\sqrt{2}-3\sqrt{2}+\dfrac{1}{3}\cdot3\sqrt{2}\)

\(=10\sqrt{2}-3\sqrt{2}+\sqrt{2}\)

\(=8\sqrt{2}\)

b) \(\dfrac{11}{4-\sqrt{5}}-\dfrac{3}{\sqrt{5}+\sqrt{2}}\)

\(=\dfrac{11\left(4+\sqrt{5}\right)}{\left(4-\sqrt{5}\right)\left(4+\sqrt{5}\right)}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)}\)

\(=\dfrac{11\left(4+\sqrt{5}\right)}{16-5}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{5-2}\)

\(=\dfrac{11\left(4+\sqrt{5}\right)}{11}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{3}\)

\(=4+\sqrt{5}-\sqrt{5}+\sqrt{2}\)

\(=4+\sqrt{2}\)

c) \(\sqrt{8-2\sqrt{15}}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)

\(=\sqrt{\left(\sqrt{5}\right)^2-2\cdot\sqrt{5}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)

\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)

\(=\left|\sqrt{5}-\sqrt{3}\right|-\left|\sqrt{5}+\sqrt{3}\right|\)

\(=\sqrt{5}-\sqrt{3}-\sqrt{5}-\sqrt{3}\)

\(=-2\sqrt{3}\)

gọi số hàng chục là X hàng đơn vị là Y

theo đề bái có: X+Y=7 (1)

nếu đổi chỗ thì được 1 số hơn số ban đầu là 27 nên ta có:

(10Y+X)-(10X+Y)=27  (2)

có hệ phương trình 

X+Y=7

(10Y+X)-(10X+Y)=27

==>giải hệ phương trình được X=2 và Y= 5

cảm ơn b nhaa