Dựa vào tính chất liên hệ giữa thứ tự và phép cộng, hãy chứng tỏ rằng: Nếu m – n > 0 thì m > n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 6 2019
Ta có: m > n ⇒ m + (-n) > n + (-n)
⇒ m – n > n – n ⇒ m – n > 0
TV
8 tháng 6 2017
Fan Soobin Hoàng Sơn
=> m = 5
Vậy m = 5
b) 343125=(75)n
⇒(75)3=(75)n
=> n = 3
Vậy n = 3
27 tháng 7 2016
a) \(\left(\frac{1}{2}\right)^m=\frac{1}{32}\)
\(=>\left(\frac{1}{2}\right)^m=\frac{1^5}{2^5}\)
\(=>\left(\frac{1}{2}\right)^m=\left(\frac{1}{2}\right)^5\)
\(=>m=5\)
b) \(\frac{343}{125}=\left(\frac{7}{5}\right)^n\)
\(=>\frac{7^3}{5^3}=\left(\frac{7}{5}\right)^n\)
\(=>\left(\frac{7}{5}\right)^3=\left(\frac{7}{5}\right)^n\)
\(=>n=3\)
27 tháng 7 2016
a) \(\left(\frac{1}{2}\right)^m=\frac{1}{32}\)
\(\Rightarrow\left(\frac{1}{2}\right)^m=\left(\frac{1}{2}\right)^5\)
=> m =5
b) \(\frac{343}{125}=\left(\frac{7}{5}\right)^n\)
\(\Rightarrow\left(\frac{7}{5}\right)^3=\left(\frac{7}{5}\right)^n\)
=> n = 3
9 tháng 3 2018
a) \(a>b\Leftrightarrow a-b>b-b=0\)
b) \(a+b>c\Leftrightarrow a+b-b>c-b\Leftrightarrow a>c-b\)
c)
Cm: \(a^2-a+3\ge a+2\)
\(\Rightarrow a^2-a+3-a-2\ge0\)
\(\Rightarrow a^2-2a+1\ge0\Leftrightarrow\left(a-1\right)^2\ge0\) *đúng*
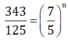
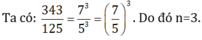
Ta có: m – n > 0 ⇒ m – n + n > 0 + n ⇒ m > n